
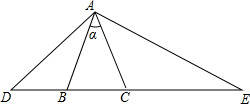
 如图,△ABC中,AB=AC,∠BAC=α,D,E分别在底边CB,BC的延长线上,当AB2=DB•CE时,求∠DAE的度数.
如图,△ABC中,AB=AC,∠BAC=α,D,E分别在底边CB,BC的延长线上,当AB2=DB•CE时,求∠DAE的度数. 分析 根据AB=AC,求得∠ABD=∠ACE,再利用AB2=DB•CE,即可得出对应边成比例,即可证得△ADB∽△EAC,得出∠BAD=∠E,∠D=∠CAE,则∠DAE=∠BAD+∠BAC+∠CAE=∠D+∠BAD+∠BAC,即可得出结果.
解答 解:∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵AB2=DB•CE
∴$\frac{AB}{CE}$=$\frac{DB}{AB}$,
∴$\frac{AB}{CE}$=$\frac{DB}{AC}$,
∴△ADB∽△EAC.
∴∠BAD=∠E,∠D=∠CAE,
∵∠DAE=∠BAD+∠BAC+∠CAE,
∴∠DAE=∠D+∠BAD+∠BAC,
∵∠BAC=α,AB=AC,
∴∠ABC=$\frac{1}{2}$(180°-α),
∴∠D+∠BAD=$\frac{1}{2}$(180°-α),
∴∠DAE=∠D+∠BAD+∠BAC=$\frac{1}{2}$(180°-α)+α=90°+$\frac{α}{2}$.
点评 本题主要考查了相似三角形的判定,等腰三角形的性质,以及学生对相似三角形的判定这一知识点的理解和掌握,难度不大,属于基础题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:选择题
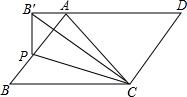 如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABOC中,对角线相交于点E,双曲线y=$\frac{k}{x}$(k<0)的一支经过C,E两点,若?ABCD的面积为10,求k的值.
如图,在?ABOC中,对角线相交于点E,双曲线y=$\frac{k}{x}$(k<0)的一支经过C,E两点,若?ABCD的面积为10,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
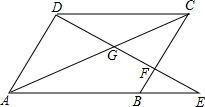 如图,四边形ABCD为平行四边形,试说明:
如图,四边形ABCD为平行四边形,试说明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com