
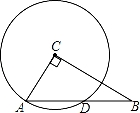
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A.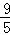 B.
B.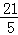 C.
C.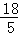 D.
D.
C【考点】垂径定理;勾股定理.
【专题】探究型.
【分析】先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长,在Rt△ACM中,根据勾股定理可求出AM的长,进而可得出结论.
【解答】解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=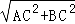 =
=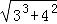 =5,
=5,
过C作CM⊥AB,交AB于点M,如图所示,
∵CM⊥AB,
∴M为AD的中点,
∵S△ABC= AC•BC=
AC•BC= AB•CM,且AC=3,BC=4,AB=5,
AB•CM,且AC=3,BC=4,AB=5,
∴CM=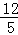 ,
,
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+(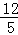 )2,
)2,
解得:AM=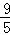 ,
,
∴AD=2AM=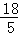 .
.
故选C.

【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
探究:中华人民共和国国旗上的五角星的每个角均相等,小明为了计算每个角的度数,画出了如图①的五角星,每个角均相等,并写出了如下不完整的计算过程,请你将过程补充完整.
解:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=__________°,
∴∠A+∠B+∠C+∠D+∠E=__________°,
∴∠A=∠B=∠C=∠D=∠E=__________°.
拓展:如图②,小明改变了这个五角星的五个角的度数,使它们均不相等,请你帮助小明求∠A、∠B、∠C、∠D、∠E的和.
应用:如图③.小明将图②中的点A落在BE上,点 C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.
C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
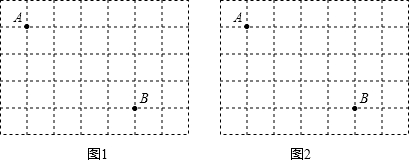
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.
(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可);
(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
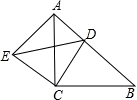
如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.
(1)求证:△ACE≌△BCD;
 (2)求证:△ADE是直角三角形;
(2)求证:△ADE是直角三角形;
(3)已知△ADE的面积为30cm2,DE=13cm,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
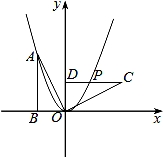
如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为 .
1
查看答案和解析>>
科目:初中数学 来源: 题型:
小明记录了一周内每天的最高气温如下表,则这个周内每天最高气温的中位数是( )
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 最高气温(℃) |
| 24 | 23 | 25 | 24 | 22 | 21 |
A. 22℃ B. 23℃ C. 24℃  D. 25℃
D. 25℃
查看答案和解析>>
科目:初中数学 来源: 题型:
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC;
①将△ABC向x轴正方向平移5个单位得△A1B1C1,
②再以O为旋转中心,将△A1B1C1旋转180°得△A2B2C2,画出平移和旋转后的图形,并标明对应字母.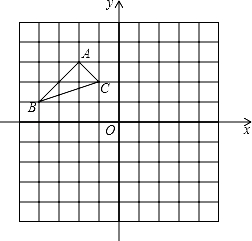
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com