
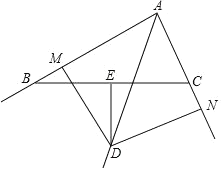
【题目】如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)求证:BM=CN;
(2)若AB=8,AC=4,求BM的长.
【答案】(1)见解析;(2)2
【解析】
(1)根据角平分线的性质和线段垂直平分线的性质可得到DM=DN,DB=DC,根据HL证明Rt△DMB≌Rt△DNC,即可得出BM=CN;
(2)由HL证明Rt△DMA≌Rt△DNA,得出AM=AN,证出2BM=AB-AC=4,即可得出BM=2.
(1)证明:连接BD、CD,如图所示:
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
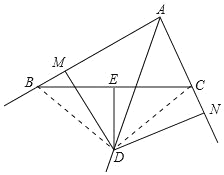
∵DE垂直平分线BC,
∴DB=DC,
在Rt△DMB和Rt△DNC中,
![]()
∴Rt△DMB≌Rt△DNC(HL),
∴BM=CN;
(2) 由(1)得:BM=CN,
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
在Rt△DMA和Rt△DNA中,
![]()
∴Rt△DMA≌Rt△DNA(HL),
∴AM=AN,
∵AM=AB-BM,AN=AC+CN,
∴AB-BM=AC+CN,
∴2BM=AB-AC=8-4=4,
∴BM=2.


科目:初中数学 来源: 题型:
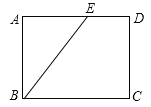
【题目】如图,矩形ABCD中,AB=1,BC=2,点E在AD上,点F在BC边上,FE平分∠DFB.

(1)判断△DEF的形状,并说明理由;
(2)若点F是BC的中点,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
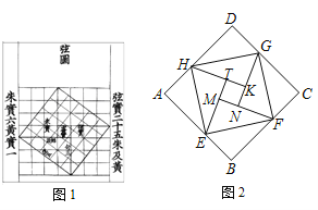
【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成. 将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为![]() ,
,![]() ,
,![]() . 若
. 若![]() , 则正方形EFGH的面积为_______.
, 则正方形EFGH的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为6cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不到点A).设点E,F同时出发移动t秒.
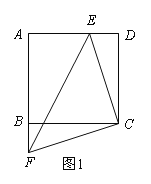

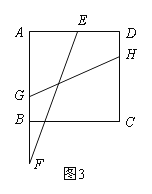
(1)在点E,F移动过程中,连接CE,CF,EF,则△CEF的形状是 ,始终保持不变;
(2)如图2,连接EF,设EF交BD于点M,当t=2时,求AM的长;
(3)如图3,点G,H分别在边AB,CD上,且GH=![]() cm,连接EF,当EF与GH的夹角为45°,求t的值.
cm,连接EF,当EF与GH的夹角为45°,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形的一个内角平分线把矩形的一条边分成3cm和5cm两部分,则矩形的周长( )
A. 16cm B. 22cm和16cm C. 26cm D. 22cm和26cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并回答问题:
我们知道,乘法公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,如:![]() ,就可以用图1或图2等图形的面积表示.
,就可以用图1或图2等图形的面积表示.
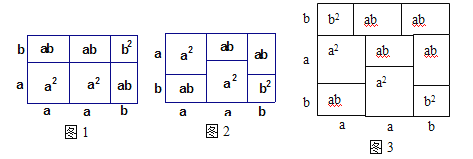
(1)请写出图3所表示的代数恒等式: ;
(2)试画一个几何图形,使它的面积表示:![]() ;
;
(3)请仿照上述方法另写一个含有![]() ,
,![]() 的代数恒等式,并画出与它对应的几何图形.
的代数恒等式,并画出与它对应的几何图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com