
����Ŀ��ij��ѧ��ȤС�鿪չ��һ�λ���������£���![]() .�ְ�С�����ΰڷ���������֮�䣬��ʹС�����˷ֱ���������
.�ְ�С�����ΰڷ���������֮�䣬��ʹС�����˷ֱ���������![]() ��
��![]() �ϣ�
�ϣ�
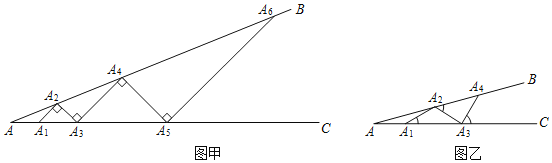
�һ����ͼ����ʾ���ӵ�![]() ��ʼ���������Ұڷ�С����ʹС����С���ڶ˵㴦���ഹֱ��
��ʼ���������Ұڷ�С����ʹС����С���ڶ˵㴦���ഹֱ��![]() Ϊ��1��С����
Ϊ��1��С����
��ѧ˼����
��1��С�������ް���ȥ�𣿴� ����ܡ����ܡ���
��2����![]() ����
����![]() �Ķ�����
�Ķ�����
�������ͼ����ʾ���ӵ�![]() ��ʼ���õȳ���С���������Ұڷţ�����
��ʼ���õȳ���С���������Ұڷţ�����![]() Ϊ��һ��С������
Ϊ��һ��С������![]() ��
��
��ѧ˼����
��3�����Ѿ��ڷ���3��С������![]() ��
��![]() ��
��![]() �����ú�
�����ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��4����ֻ�ܰڷ�5��С������![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
���𰸡���1���ܣ���2������22.5�㣻��3��2����3����4������4��15�������18�㣮
��������
��1����С����С���ڶ˵㴦���ഹֱ�����ɵõ��𰸣�
��2�����ݵ���ֱ�������ε����ʺ���������ǵ����ʣ����ɵõ��𰸣�
��3����![]() ���á�AA2A1=��A2AA1=�����Ӷ���
���á�AA2A1=��A2AA1=�����Ӷ���![]() ��AA2A1+��A2AA1=2����ͬ����
��AA2A1+��A2AA1=2����ͬ����![]() ��A2AA1+
��A2AA1+![]() =��+2��=3�ȣ�
=��+2��=3�ȣ�![]() ��A2AA1+
��A2AA1+![]() ��+3��=4�ȣ�
��+3��=4�ȣ�
��4����������ã�5����90����6����90�㣬�������ɵõ��𰸣�
��1����С����С���ڶ˵㴦���ഹֱ���ɣ�
��С�������ް���ȥ��
�ʴ��ǣ��ܣ�
��2����A1A2��A2A3��A1A2��A2A3��
���A2A1A3��45�㣬
���AA2A1+����45�㣬
��AA1��A1A2
���AA2A1����BAC=����
������22.5�㣻
��3����![]() ��
��
���AA2A1=��A2AA1=����
��![]() ��AA2A1+��A2AA1=2����
��AA2A1+��A2AA1=2����
��![]() ��
��
��![]()
![]() =2�ȣ�
=2�ȣ�
��![]() ��A2AA1+
��A2AA1+![]() =��+2��=3�ȣ�
=��+2��=3�ȣ�
��![]() ��
��
��![]()
![]() 3�ȣ�
3�ȣ�
��![]() ��A2AA1+
��A2AA1+![]() ��+3��=4�ȣ�
��+3��=4�ȣ�
�ʴ��ǣ�2����3����4����
��4���ɵڣ�3����ɵã�![]() 5�ȣ�
5�ȣ�![]() 6�ȣ�
6�ȣ�
��ֻ�ܰڷ�5��С����
��5����90����6����90�㣬
��15�������18�㣮
�ʴ��ǣ�15�������18�㣮


 �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д� ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��x+m��y��nx��5n��n��0���Ľ���ĺ�����Ϊ3�������x�IJ���ʽx+m��nx��5n��0��������Ϊ�� ��
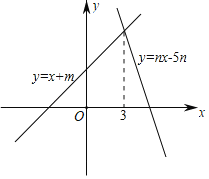
A.3B.4C.5D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() ���ң�
���ң�![]() Ϊ
Ϊ![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��
![]() ��֤��
��֤��![]() ��
��![]() �����ߣ�
�����ߣ�
![]() ���
���![]() ��
��![]() ��
��![]() ����
����![]() �뾶�ij���
�뾶�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
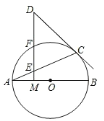
����Ŀ����ͼ��AD��AC�ֱ��ǡ�O��ֱ�����ң��ҡ�CAD=30�㣮OB��AD��AC�ڵ�B����OB=4����BC��Ϊ��������
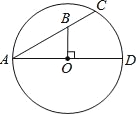
A. 2 B. 3 C. 3.6 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
����x�ķ��̣�x+![]() ��c+
��c+![]() �Ľ�Ϊx1��c��x2��
�Ľ�Ϊx1��c��x2��![]() ��x��
��x��![]() ��c��
��c��![]() ���ɱ���Ϊx+
���ɱ���Ϊx+![]() ��c+
��c+![]() ���Ľ�Ϊx1��c��x2��
���Ľ�Ϊx1��c��x2��![]() ��x+
��x+![]() ��c+
��c+![]() �Ľ�Ϊx1��c��x2��
�Ľ�Ϊx1��c��x2��![]() Zx+
Zx+![]() ��c+
��c+![]() �Ľ�Ϊx1��c��x2��
�Ľ�Ϊx1��c��x2��![]() Z.
Z.
��1�����ɽ��ۣ������������������������õ�����x�ķ���x+![]() ��c+
��c+![]() ��m��0���Ľ�Ϊ�� ����
��m��0���Ľ�Ϊ�� ����
��2��Ӧ�ý��ۣ������y�ķ���y��a��![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A=65����B=75����ֽƬһ���۵���ʹ��C������ABC�⣬����2=20�����1�Ķ���Ϊ _______.
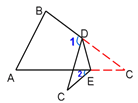
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�BC=a��AC=b��AB=c����D��BC��AC��AB�����У��е�ֱ���E��F��G��BA��ED���ӳ��߽��ڵ�H��a��b�ǹ���x�ķ���x2����c+4��x+4c+8=0����������
(1)��֤����ABC��ֱ�������Σ�
(2)��25asin��BAC=9c�����ı���CEDF�������
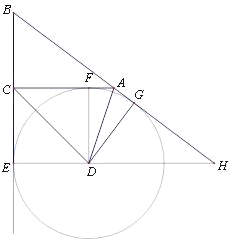
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㳦��®���ش��ڵĴ�ͳϰ�ף�С�ϵĸ���ȥ�괺��ǰ����![]() Ԫ��������װ�㳦�������°����ܷ�������Ӱ�죬������ִ�����Ǽۣ��۸��ȥ��������
Ԫ��������װ�㳦�������°����ܷ�������Ӱ�죬������ִ�����Ǽۣ��۸��ȥ��������![]() Ԫ
Ԫ![]() ��
��
��1�����ȥ������۸�Ϊ![]() Ԫ
Ԫ![]() �������
�������![]() Ԫ��ȥ���������
Ԫ��ȥ���������![]() ���⣿(�����
���⣿(�����![]() ��ʽ�ӱ�ʾ)
��ʽ�ӱ�ʾ)
��2������������Ϊ���������г���Ӧ��Ϊ�����������룬��ȡһϵ�л������ߣ�����۸��½���![]() Ԫ
Ԫ![]() ������С�ϵĸ�����
������С�ϵĸ�����![]() ��ȥ��һ��������⣮��С�ϸ����깺������ÿǧ�˶���Ԫ��
��ȥ��һ��������⣮��С�ϸ����깺������ÿǧ�˶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() �У�
�У�![]() ������Ϊ
������Ϊ![]() ��
��![]() ƽ��
ƽ��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ
Ϊ![]() �ϵ�һ�㣬����
�ϵ�һ�㣬����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��1����![]() ��
��![]() ����
����![]() ��
��![]() �ij���
�ij���
��2����֤��![]() ��
��
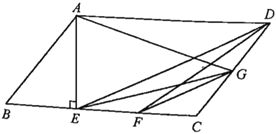
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com