
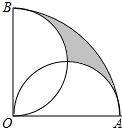
 如图,在半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{π}{2}$-1.
如图,在半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{π}{2}$-1. 分析 假设出扇形半径,再表示出半圆面积,以及扇形面积,进而即可表示出两部分P,Q面积相等.连接AB,OD,根据两半圆的直径相等可知∠AOD=∠BOD=45°,故可得出绿色部分的面积=S△AOD,利用阴影部分Q的面积为:S扇形AOB-S半圆-S绿色,故可得出结论.
解答 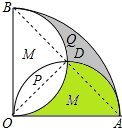 解:∵扇形OAB的圆心角为90°,扇形半径为2,
解:∵扇形OAB的圆心角为90°,扇形半径为2,
∴扇形面积为:$\frac{90π×{2}^{2}}{360}$=π(cm2),
半圆面积为:$\frac{1}{2}$×π×12=$\frac{π}{2}$(cm2),
∴SQ+SM =SM+SP=$\frac{π}{2}$(cm2),
∴SQ=SP,
连接AB,OD,
∵两半圆的直径相等,
∴∠AOD=∠BOD=45°,
∴S绿色=S△AOD=$\frac{1}{2}$×2×1=1(cm2),
∴阴影部分Q的面积为:S扇形AOB-S半圆-S绿色=π-$\frac{π}{2}$-1=$\frac{π}{2}$-1(cm2).
故答案为:$\frac{π}{2}$-1.
点评 此题主要考查了扇形面积求法,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
 为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.
为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.| 各种情况人数统计频数分布表 | ||||
| 课外阅读情况 | A | B | C | D |
| 频数 | 20 | x | y | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com