
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交BC、AC于点D、E.
(1)若AC=12,BC=15,求△ABD的周长;
(2)若∠B=20°,求∠BAD的度数.

【答案】(1)27;(2)120°.
【解析】
试题(1)根据线段垂直平分线性质求出AD=DC,求出△ABD周长=AB+BC即可;
(2)根据等腰三角形性质求出∠C,∠DAC,根据三角形内角和定理求出∠BAC,即可求出答案.
试题解析:(1)∵AC的垂直平分线分别交BC、AC于点D、E,
∴AD=DC,
∵AB=AC=12,
∴△ABD的周长为AB+AD+BD=AB+DC+BD=AB+BC=12+15=27;
(2)∵AB=AC,∠B=20°,
∴∠C=∠B=20°,
∴∠BAC=180°-20°-20°=140°,
∵AD=DC,
∴∠DAC=∠C=20°,
∴∠BAD=∠BAC-∠DAC=140°-20°=120°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
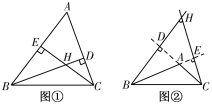
【题目】(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H.找出∠BHC和∠A之间存在何种等量关系;
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,把图②补充完整,并指出此时(1)中的等量关系是否仍然成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN. 
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是直角三角形,∠A=90°,D是斜边BC的中点,E、F分别是AB、AC边上的动点,且DE⊥DF.
(1)如图1,AB=AC,BE=12,CF=5,求线段EF的长.
(2)如图2,若AB≠AC,写出线段EF与线段BE、CF之间的等量关系,并写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=﹣2x2﹣1向上平移若干个单位,使抛物线与坐标轴有三个交点,如果这些交点能构成直角三角形,那么平移的距离为( )
A.![]() 个单位
个单位
B.1个单位
C.![]() 个单位
个单位
D.![]() 个单位
个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知非直角三角形ABC中,∠A=45°,高BD与CE所在直线交于点H,则∠BHC的度数是( )
A. 45° B. 45° 或125° C. 45°或135° D. 135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com