
【题目】如图,平面内的两条直线l1、l2,点A、B在直线l2上,过点A、B两点分别作直线l1的垂线,垂足分别为A1、B1,我们把线段A1B1叫做线段AB在直线l2上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线l2上的正投影就是线段A1C,请依据上述定义解决如下问题.
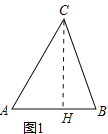
(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;
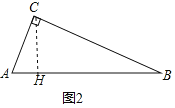
(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;
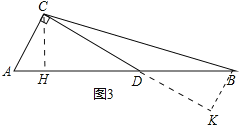
(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,CD).


【答案】(1)2 ;(2)△ABC的面积=39;(3)T(BC,CD)=![]()
【解析】
(1)如图1,过C作CH⊥AB,根据正投影的定义求出BH的长即可;
(2)如图2,过点C作CH⊥AB于H,由正投影的定义可知AH=4,BH=9,再根据相似三角形的性质求出CH的长即可解决问题;
(3)如图3,过C作CH⊥AB于H,过B作BK⊥CD于K,求出CD、DK即可得答案.
(1)如图1,过C作CH⊥AB,垂足为H,
∵T(AC,AB)=3,
∴AH=3,
∵AB=5,
∴BH=AB-AH=2,
∴T(BC,AB)=BH=2,
故答案为:2;
(2)如图2,过点C作CH⊥AB于H,
则∠AHC=∠CHB=90°,
∴∠B+∠HCB=90°,
∵∠ACB=90°,
∴∠B+∠A=90°
∴∠A=∠HCB,
∴△ACH∽△CBH,
∴CH:BH=AH:CH,
∴CH2=AH·BH,
∵T(AC,AB)=4,T(BC,AB)=9,
∴AH=4,BH=9,
∴AB=AH+BH=13,CH=6,
∴S△ABC=(AB·CH)÷2=13×6÷2=39;
(3)如图3,过C作CH⊥AB于H,过B作BK⊥CD于K,
∵∠ACD=90°,T(AD,AC)=2,
∴AC=2,
∵∠A=60°,
∴∠ADC=∠BDK=30°,
∴CD=AC·tan60°=2![]() ,AD=2AC=4,AH=
,AD=2AC=4,AH=![]() AC=1,
AC=1,
∴DH=4-1=3,
∵T(BC,AB)=6,CH⊥AB,
∴BH=6,
∴DB=BH-DH=3,
在Rt△BDK中,∠K=90°,BD=3,∠BDK=30°,
∴DK=BD·cos30°=![]() ,
,
∴T(BC,CD)=CK=CD+DK=![]() +
+![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价![]() (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)
(2)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
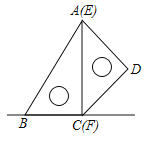
【题目】如图,一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 拼合在一个平面上,边
拼合在一个平面上,边![]() 与
与![]() 重合,
重合,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 方向滑动时,点
方向滑动时,点![]() 同时从点
同时从点![]() 出发沿射线
出发沿射线![]() 方向滑动.当点
方向滑动.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,点
时,点![]() 运动的路径长为______
运动的路径长为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣2x2﹣4x+6.
(1)用配方法求出函数的顶点坐标;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
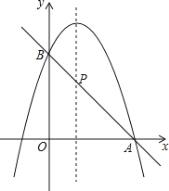
【题目】如图,二次函数y=﹣x2+2x+m的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P.
(1)求点B的坐标;
(2)求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=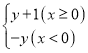 ,则称点Q为点P的“亲密点”.例如:点(1,2)的“亲密点”为点(1,3),点(﹣1,3)的“亲密点”为点(﹣1,﹣3).若点P在函数y=x2﹣2x﹣3的图象上,则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是( )
,则称点Q为点P的“亲密点”.例如:点(1,2)的“亲密点”为点(1,3),点(﹣1,3)的“亲密点”为点(﹣1,﹣3).若点P在函数y=x2﹣2x﹣3的图象上,则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是( )
A.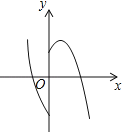 B.
B.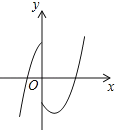
C.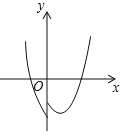 D.
D.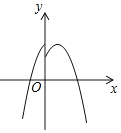
查看答案和解析>>
科目:初中数学 来源: 题型:
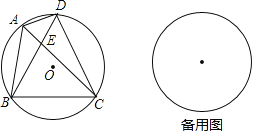
【题目】如图,四边形ABCD内接于⊙O.
(1)连接AC、BD,若∠BAC=∠CAD=60°,则△DBC的形状为 .
(2)在(1)的条件下,试探究线段AD,AB,AC之间的数量关系,并证明你的结论;
(3)若![]() ,∠DAB=∠ABC=90°,点P为
,∠DAB=∠ABC=90°,点P为![]() 上的一动点,连接PA,PB,PD,求证:PD=PB+
上的一动点,连接PA,PB,PD,求证:PD=PB+![]() PA.
PA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于点D,点F为AB上一点,连接CF,过点B作BE⊥BC交CF的延长线于点E,交AD于点H,且∠1=∠2
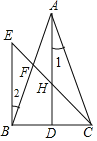
(1)求证:AB=AC;
(2)若∠1=22°,∠AFC=110°,求∠BCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】淇淇和嘉嘉在学习了利用相似三角形测高之后分别测量两个旗杆高度.
(1)如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,已知淇淇同学的身高是1.54m,眼睛位置A距离淇淇头顶的距离是4cm,求旗杆DE 的高度.

如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为![]() 米,∠DCE=45°,求旗杆AB的高度?
米,∠DCE=45°,求旗杆AB的高度?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com