
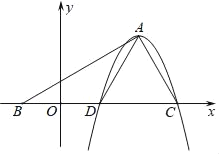
【题目】定义:若抛物线的顶点和与x轴的两个交点所组成的三角形为等边三角形时.则称此抛物线为正抛物线.
概念理解:
(1)如图,在△ABC中,∠BAC=90°,点D是BC的中点.试证明:以点A为顶点,且与x轴交于D、C两点的抛物线是正抛物线;
问题探究:
(2)已知一条抛物线经过x轴的两点E、F(E在F的左边),E(1,0)且EF=2若此条抛物线为正抛物线,求这条抛物线的解析式;
应用拓展:
(3)将抛物线y1=﹣x2+2![]() x+9向下平移9个单位后得新的抛物线y2.抛物线y2的顶点为P,与x轴的两个交点分别为M、N(M在N左侧),把△PMN沿x轴正半轴无滑动翻滚,当边PN与x轴重合时记为第1次翻滚,当边PM与x轴重合时记为第2次翻滚,依此类推…,请求出当第2019次翻滚后抛物线y2的顶点P的对应点坐标.
x+9向下平移9个单位后得新的抛物线y2.抛物线y2的顶点为P,与x轴的两个交点分别为M、N(M在N左侧),把△PMN沿x轴正半轴无滑动翻滚,当边PN与x轴重合时记为第1次翻滚,当边PM与x轴重合时记为第2次翻滚,依此类推…,请求出当第2019次翻滚后抛物线y2的顶点P的对应点坐标.
【答案】(1)详见解析;(2)y=![]() 或y=
或y=![]() ;(3)当第2019次翻滚后抛物线y2的顶点P的对应点坐标为(4039
;(3)当第2019次翻滚后抛物线y2的顶点P的对应点坐标为(4039![]() ,3).
,3).
【解析】
(1)由Rt△ABC中AD是斜边BC的中线可得AD=CD,由抛物线对称性可得AD=AC,即证得△ACD是等边三角形.
(2)设抛物线顶点为G,根据正抛物线定义得△EFG是等边三角形,又易求E、F坐标,即能求G点坐标.由于不确定点G纵坐标的正负号,故需分类讨论,再利用顶点式求抛物线解析式.
(3)根据题意求出抛物线y2的解析式,并按题意求出P、M、N的坐标,得到等边△PMN,所以当△PMN翻滚时,每3次为一个周期,点P回到x轴上方,且横坐标每多一个周期即加6![]() ,其规律为当翻滚次数n能被3整除时,横坐标为:
,其规律为当翻滚次数n能被3整除时,横坐标为:![]() +n×2
+n×2![]() =(2n+1)
=(2n+1)![]() .2019能被3整除,代入即能求此时点P坐标.
.2019能被3整除,代入即能求此时点P坐标.
解:(1)证明:∠BAC=90°,点D是BC的中点
∴AD=BD=CD=![]() BC
BC
∵抛物线以A为顶点与x轴交于D、C两点
∴AD=AC
∴AD=AC=CD
∴△ACD是等边三角形
∴以A为顶点与x轴交于D、C两点的抛物线是正抛物线.
(2)∵E(1,0)且EF=2,点F在x轴上且E在F的左边
∴F(3,0)
∵一条经过x轴的两点E、F的抛物线为正抛物线,设顶点为G
∴△EFG是等边三角形
∴xG=![]()
①当G(2,![]() )时,设抛物线解析式为y=a(x﹣2)2+
)时,设抛物线解析式为y=a(x﹣2)2+![]()
把点E(1,0)代入得:a+![]() =0
=0
∴a=﹣![]()
∴y=﹣![]() (x﹣2)2+
(x﹣2)2+![]()
②当G(2,﹣![]() )时,设抛物线解析式为y=a(x﹣2)2﹣
)时,设抛物线解析式为y=a(x﹣2)2﹣![]()
把点E(1,0)代入得:a﹣![]() =0
=0
∴a=![]()
∴y=![]() (x﹣2)2﹣
(x﹣2)2﹣![]()
综上所述,这条抛物线的解析式为y=﹣![]() (x﹣2)2+
(x﹣2)2+![]() 或y=
或y=![]() (x﹣2)2﹣
(x﹣2)2﹣![]()
(3)∵抛物线y1=﹣x2+2![]() x+9=﹣(x﹣
x+9=﹣(x﹣![]() )2+12
)2+12
∴y1向下平移9个单位后得抛物线y2=﹣(x﹣![]() )2+3
)2+3
∴P(![]() ,3),M(0,0),N(2
,3),M(0,0),N(2![]() ,0)
,0)
∴PM=MN=PN=2![]()
∴△PMN是等边三角形
∴第一次翻滚顶点P的坐标变为P1(4![]() ,0),第二次翻滚得P2与P1相同,第三次翻滚得P3(7
,0),第二次翻滚得P2与P1相同,第三次翻滚得P3(7![]() ,3)
,3)
即每翻滚3次为一个周期,当翻滚次数n能被3整除时,点P纵坐标为3,横坐标为:![]() +n×2
+n×2![]() =(2n+1)
=(2n+1)![]()
∵2019÷3=673
∴(2×2019+1)×![]() =4039
=4039![]()
∴当第2019次翻滚后抛物线y2的顶点P的对应点坐标为(4039![]() ,3).
,3).


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
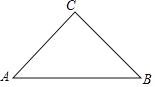
【题目】如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
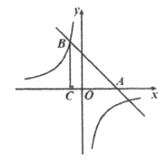
【题目】如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 的一个交点为B(-1,4).
的一个交点为B(-1,4).
(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线![]() 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上, 顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为__ _.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
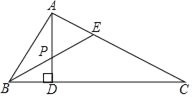
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了求1+2+22+23+…+22016+22017的值,
可令S=1+2+22+23+…+22016+22017,
则2S=2+22+23+24+…+22017+22018,
因此2S﹣S=22018﹣1,
所以1+22+23+…+22017=22018﹣1.
请你仿照以上方法计算1+5+52+53+…+52017的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() 出现了错误,解答过程如下:
出现了错误,解答过程如下:
方程两边都乘以![]() ,得
,得![]() (第一步)
(第一步)
去括号,得![]() (第二步)
(第二步)
移项,合并同类项,得![]() (第三步)
(第三步)
解得![]() (第四步)
(第四步)
![]() 原方程的解为
原方程的解为![]() (第五步)
(第五步)
(1)小明解答过程是从第_____步开始出错的,这一步正确的解答结果_____,此步的根据是_____.
(2)小明的解答过程缺少_____步骤,此方程的解为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E为长方形纸片ABCD的边CD上一点,将纸片沿AE对折,点D的对应点D′恰好在线段BE上.若AD=3,DE=1,则AB=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com