
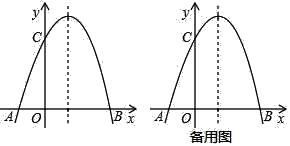
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).
(1)求抛物线的解析式;
(2)设点M在抛物线的对称轴上,当△MAC是以AC为直角边的直角三角形时,求点M的坐标.
【答案】(1)y=﹣x2+2x+3;(2)当△MAC是直角三角形时,点M的坐标为(1,![]() )或(1,﹣
)或(1,﹣![]() ).
).
【解析】
(1)由点A、C的坐标,利用待定系数法即可求出抛物线的解析式;
(2)设点M的坐标为(1,m),则CM=![]() ,AC=
,AC=![]() ,AM=
,AM=![]() ,分∠ACM=90°和∠CAM=90°两种情况,利用勾股定理可得出关于m的方程,解之可得出m的值,进而即可得出点M的坐标.
,分∠ACM=90°和∠CAM=90°两种情况,利用勾股定理可得出关于m的方程,解之可得出m的值,进而即可得出点M的坐标.
(1)将A(﹣1,0)、C(0,3)代入y=﹣x2+bx+c中,
得:![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
设点M的坐标为(1,m),
则CM=![]() ,AC=
,AC=![]() =
=![]() ,AM=
,AM=![]() .
.
分两种情况考虑:
①当∠ACM=90°时,有AM2=AC2+CM2,即4+m2=10+1+(m﹣3)2,
解得:m=![]() ,
,
∴点M的坐标为(1,![]() );
);
②当∠CAM=90°时,有CM2=AM2+AC2,即1+(m﹣3)2=4+m2+10,
解得:m=﹣![]() ,
,
∴点M的坐标为(1,﹣![]() ).
).
综上所述:当△MAC是直角三角形时,点M的坐标为(1,![]() )或(1,﹣
)或(1,﹣![]() ).
).


科目:初中数学 来源: 题型:
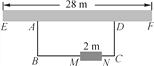
【题目】如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).现有砌60米长的墙的材料.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成480平方米的矩形花园,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
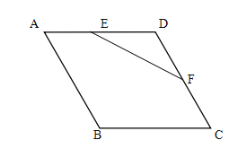
【题目】如图,菱形ABCD的边长为8,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,且AE+CF=8,则△DEF面积的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强身体素质,小明每天早上坚持沿着小区附近的矩形公园ABCD练习跑步,爸爸站在的某一个固定点处负责进行计时指导。假设小明在矩形公园ABCD的边上沿着A→B→C→D→A的方向跑步一周,小明跑步的路程为x米,小明与爸爸之间的距离为y米.y与x之间的函数关系如图2所示,则爸爸所在的位置可能为图1的( )
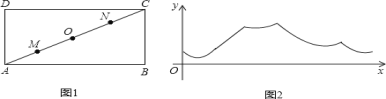
A. D点B. M点C. O点D. N点
查看答案和解析>>
科目:初中数学 来源: 题型:
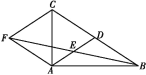
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的条件下,要使四边形ADCF为正方形,在△ABC中应添加什么条件,请直接把补充条件写在横线上 (不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com