
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2.
(1)求OD的长.
(2)求EC的长.

【答案】(1)5 (2)![]()
【解析】
(1)设⊙O的半径为r,根据垂径定理求出AC的长,在Rt△OAC中利用勾股定理求出r的值;
(2)连接BE,由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中利用勾股定理可计算出CE.
解:(1)设⊙O半径为r,则OA=OD=r,OC=r﹣2,
∵OD⊥AB,
∴∠ACO=90°,
AC=BC=![]() AB=4,
AB=4,
在Rt△ACO中,由勾股定理得:r2=42+(r﹣2)2,
r=5,
∴OD=r=5;
(2)连接BE,如图:

由(1)得:AE=2r=10,
∵AE为⊙O的直径,
∴∠ABE=90°,
由勾股定理得:BE=6,
在Rt△ECB中,EC=![]() =
=![]() =2
=2![]() .
.
故答案为:(1)5;(2)![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?

查看答案和解析>>
科目:初中数学 来源: 题型:
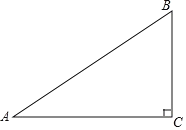
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(![]() )
)![]() ,正六边形的边长为(
,正六边形的边长为(![]() )cm(其中
)cm(其中![]() ),求这两段铁丝的总长
),求这两段铁丝的总长

查看答案和解析>>
科目:初中数学 来源: 题型:
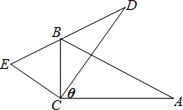
【题目】如图,△ABC中,∠ACB=90°,∠A=25°,若以点C为旋转中心,将△ABC旋转θ度到△DEC的位置,使点B恰好落在边DE上,则θ等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D
(1) 求证:DP=DB
(2) 求证:DA+DB=DC
(3) 若等边△ABC边长为![]() ,连接BH,当△BDH为等边三角形时,请直接写出CP的长度为_________
,连接BH,当△BDH为等边三角形时,请直接写出CP的长度为_________

查看答案和解析>>
科目:初中数学 来源: 题型:
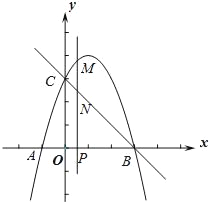
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式和直线BC的解析式;
(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;
(3)当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧AC中点,BD交AC于点E.
(1)求证:AD2=DEDB;
(2)若BC=13,CD=5,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
①(x+1)2=4x
②x2+3x﹣4=0(用配方法)
③x2﹣2x﹣8=0
④2(x+4)2=5(x+4)
⑤2x2﹣7x=4
⑥(x+1)(x+2)=2x+4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com