Question

【题目】中，，，，为上一点，为上一点，且，分别于、相切，则的半径为（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】

由勾股定理求出AB=10，连接FP、PE，过P作PM⊥AC于M，根据切线的性质得出矩形CMPF，推出PM=CF，PF=CM，设圆P的半径是r，根据切线的性质和切线长定理、等腰三角形的性质得到DF=FP，AM=PM，BE=BF，根据勾股定理得出AP2=AE2+PE2=AM2+PM2，代入即可得到方程，求出方程的解即可．

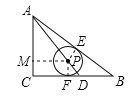
由勾股定理得：AB==10，

连接FP、PE，过P作PM⊥AC于M，

∵∠C=90°，PF⊥BC，

∴四边形CMPF是矩形，

∴PM=CF，PF=CM，

设圆P的半径是r，

∵AC=CD，∠C=90°，

∴∠ADC=45°，

∵PF⊥BC，

∴∠FPD=45°=∠ADC，

∴DF=FP=r，

同理：AM=PM，

∵圆P切AB于E，切BC于F，

∴BF=BE=BD+DF=8-6+r，

∴AE=10-（8-6+r）=8-r，

由勾股定理得：AP2=AE2+PE2=AM2+PM2，

∴（6-r）2+（6-r）2=r2+（8-r）2，

解得：r=1，

故选A．