
【题目】某商场今年1~5月的商品销售总额一共是410万元,图①表示的是其中每个月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,下列说法不正确的是( )


A. 4月份商场的商品销售总额是75万元 B. 1月份商场服装部的销售额是22万元
C. 5月份商场服装部的销售额比4月份减少了 D. 3月份商场服装部的销售额比2月份减少了
【答案】C
【解析】
用总销售额减去其他月份的销售额即可得到4月份的销售额,即可判断A;用1月份的销售总额乘以商场服装部1月份销售额占商场当月销售总额的百分比,即可判断B;分别求出4月份与5月份商场服装部的销售额,即可判断C.分别求出2月份与3月份商场服装部的销售额,即可判断D.
A、∵商场今年1-5月的商品销售总额一共是410万元,
∴4月份销售总额=410-100-90-65-80=75(万元).
故本选项正确,不符合题意;
B、∵商场服装部1月份销售额占商场当月销售总额的22%,
∴1月份商场服装部的销售额是100×22%=22(万元).故本选项正确,不符合题意;
C、∵4月份商场服装部的销售额是75×17%=12.75(万元),
5月份商场服装部的销售额是80×16%=12.8(万元),
∴5月份商场服装部的销售额比4月份增加了.
故本选项错误,符合题意;
所以C选项是正确的.
D、∵2月份商场服装部的销售额是90×14%=12.6(万元),
3月份商场服装部的销售额是65×12%=7.8(万元),
∴3月份商场服装部的销售额比2月份减少了.
故本选项正确,不符合题意.股选C.


科目:初中数学 来源: 题型:
【题目】已知,直线![]() ,E为AB、CD间的一点,连接EA、EC.
,E为AB、CD间的一点,连接EA、EC.
![]() 如图
如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
![]() 如图
如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
![]() 如图
如图![]() ,若
,若![]() ,
,![]() ,则
,则![]() ,
,![]() 与
与![]() 之间有何等量关系
之间有何等量关系![]() 并简要说明.
并简要说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
A.4﹣6小时
B.6﹣8小时
C.8﹣10小时
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83
乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是 , 乙成绩的平均数是;
(2)经计算知S甲2=6,S乙2=42.你认为选拔谁参加比赛更合适,说明理由;
(3)如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.
求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“沥园文学”社成员来自初一、初二、初三三个年级的学生,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自初一的学生为10人,则下列说法不正确的是( )

A. 扇形甲的圆心角是72° B. 学生的总人数是90人
C. 初三的人数比初二的人数多10人 D. 初一的人数比初三的人数少15人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=kx+b的图象与反比例函数![]() 的图象交于A、B两点, 且点A的坐标为(-2,3),点B的纵坐标是-2,求:
的图象交于A、B两点, 且点A的坐标为(-2,3),点B的纵坐标是-2,求:
(1)一次函数与反比例函数的解析式;
(2)利用图像指出,当![]() 为何值时有
为何值时有![]() >
>![]() ;当
;当![]() 为何值时有
为何值时有![]() <
<![]()
(3)利用图像指出,当![]() >3时
>3时![]() 的取值范围。
的取值范围。

【答案】见解析
【解析】试题分析:(1)把A点坐标代入反比例函数解析式求出m的值,把B点的纵坐标代入反比例函数解析式求出B点的横坐标,再把A、B两点的坐标代入一次函数解析式求出k、b的值即可;
(2)根据A、B的横坐标,结合图象即可得出答案;
(3)求出x=3时y2的值,然后结合图象即可得出y2的取值范围.
试题解析:
解:(1)∵A(-2,3)在反比例函数y2=![]() 的图象上,
的图象上,
∴m=-2×3
=-6,
即反比例函数的解析式为y2=![]() .
.
当y2=-2时,x=3,
即B(3,-2),
把A(-2,3),B(3,-2)代入y=kx+b得:
![]() ,
,
解得: ![]() ,
,
即一次函数的解析式为y=-x+1;
(2)结合图象可得y1>y2时对应的图象在点A的左侧和y轴与点B之间,
即x<-2或0<x<3;
同理y1<y2时对应的图象在点A与y轴之间和点B的右侧,
即-2<x<0或x>3;
(3)当x=3时,y2=-2,
当x>3时反比例函数对应的图象在点B的右侧部分,
对应的函数值-2<y2<0.
点睛:本题考查了一次函数与反比例函数的交点问题,用待定系数法求一次函数的解析式等知识点,主要考查学生的计算能力和观察图形的能力,用了数形结合思想.
【题型】解答题
【结束】
26
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,4).反比例函数![]() (x>0)的图像经过点D,点P是一次函数y=ax+4-4a(a
(x>0)的图像经过点D,点P是一次函数y=ax+4-4a(a![]() 0)的图像与该反比例函数图像的一个公共点.
0)的图像与该反比例函数图像的一个公共点.
(1)求反比例函数的表达式;
(2)一次函数y=ax+4-4a(a![]() 0)的图像恒过一定点,直接写出这个定点的坐标.
0)的图像恒过一定点,直接写出这个定点的坐标.
(3)对于一次函数y=ax+4-4a(a![]() 0),当y随x的增大而减小时,确定点P的横坐标的取值范围.(不必写出过程)
0),当y随x的增大而减小时,确定点P的横坐标的取值范围.(不必写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
A.②④⑤⑥
B.①③⑤⑥
C.②③④⑥
D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.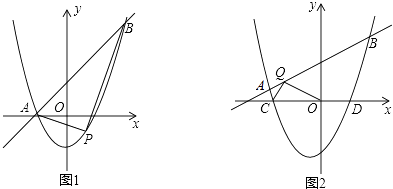
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com