
【题目】在平面直角坐标系xOy中,抛物线y=mx2+2mx﹣3(m>0)与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,该抛物线的顶点D的纵坐标是﹣4.
(1)求点A、B的坐标;
(2)设直线与直线AC关于该抛物线的对称轴对称,求直线的表达式;
(3)平行于x轴的直线b与抛物线交于点M(x1,y1)、N(x2,y2),与直线交于点P(x3,y3).若x1<x3<x2,结合函数图象,求x1+x2+x3的取值范围.
【答案】(1)A(﹣3,0)B(1,0);(2)直线的表达式为y=x﹣1;(3)﹣4<x1+x2+x3<﹣1.
【解析】
(1)根据题意求得m=1,从而求得解析式,令y=0,解方程即可求得A、B的坐标;
(2)根据轴对称求得对称点的坐标,然后根据待定系数法即可求得;
(3)由 ![]() 1,得出x1+x2=2,由题意可知2<x3<1,即可求得4<x1+x2+x3<1.
1,得出x1+x2=2,由题意可知2<x3<1,即可求得4<x1+x2+x3<1.
解:(1)∵抛物线 y=mx2+2mx﹣3(m>0)的顶点D的纵坐标是﹣4,
∴![]() 4,解得m=1,
4,解得m=1,
∴y=x2+2x﹣3,
令y=0,则 x=﹣3或1,
∴A(﹣3,0)B(1,0);
(2)∵y=x2+2x﹣3=(x+1)2﹣4,
∴抛物线的对称轴为x=﹣1,
∵点C(0,﹣3)关于抛物线的对称轴的对称点坐标是E(﹣2,﹣3),点A(﹣3,0)关于该抛物线的对称轴的对称点坐标是B(1,0),
设直线的表达式为y=kx+b,
∵点E(﹣2,﹣3)和点B(1,0)在直线上
∴![]() ,解得
,解得![]() ,
,
∴直线的表达式为y=x﹣1;
(3)由对称性可知 ![]() 1,
1,
∴x1+x2=﹣2,
∵x1<x3<x2,
∴﹣2<x3<1,
∴﹣4<x1+x2+x3<﹣1.



 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )
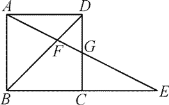
A. 6B. 8
C. 10D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育部基础教育司负责人解读“2020新中考”时强调要注重学生分析与解决问题的能力,要增强学生的创新精神和综合素质.王老师想尝试改变教学方法,将以往教会学生做题改为引导学生会学习.于是她在菱形的学习中,引导同学们解决菱形中的一个问题时,采用了以下过程(请解决王老师提出的问题):
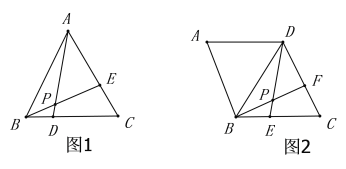
先出示问题(1):如图1,在等边三角形![]() 中,
中,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 上一点,如果
上一点,如果![]() ,连接
,连接![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,求
,求![]() 的度数.
的度数.
通过学习,王老师请同学们说说自己的收获.小明说发现一个结论:在这个等边三角形![]() 中,只要满足
中,只要满足![]() ,则
,则![]() 的度数就是一个定值,不会发生改变.紧接着王老师出示了问题(2):如图2,在菱形
的度数就是一个定值,不会发生改变.紧接着王老师出示了问题(2):如图2,在菱形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 上一点,
上一点,![]() ,连接
,连接![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,如果
,如果![]() ,
,![]() ,求出菱形的边长.
,求出菱形的边长.
问题(3):通过以上的学习请写出你得到的启示(一条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于E.
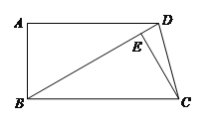
(1)求证:BE=AD;(2)若∠DCE=15°,AB=2,求在四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小刚和小红打算各自随机选择本周日的上午或下午去扬州马可波罗花世界游玩.
![]() 小明和小刚都在本周日上午去游玩的概率为________;
小明和小刚都在本周日上午去游玩的概率为________;
![]() 求他们三人在同一个半天去游玩的概率.
求他们三人在同一个半天去游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点B的坐标为![]() ,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数
,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数![]() 的图象交AB,BC分别于点E,F.
的图象交AB,BC分别于点E,F.
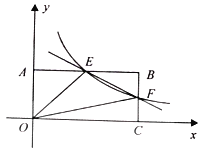
(1)求直线EF的解析式.
(2)求四边形BEOF的面积.
(3)若点P在y轴上,且![]() 是等腰三角形,请直接写出点P的坐标.
是等腰三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平行四边形ABCD中,AB︰BC=3︰2.
(1)根据条件画图:作∠BCD的平分线,交边AB于点E,取线段BE的中点F,连接DF交CE于点G.
(2)设![]() ,那么向量
,那么向量![]() =______.(用向量
=______.(用向量![]() 、
、![]() 表示),并在图中画出向量
表示),并在图中画出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com