
°æƒø°øΩÔ˝≤øª˘¥°ΩÔ˝Àæ∏∫‘»ÀΩ‚∂¡°∞2020–¬÷–øº°± ±«øµ˜“™◊¢÷ÿ—ß…˙∑÷Œˆ”ÎΩ‚æˆŒ µƒƒÐ¡¶£¨“™‘ˆ«ø—ß…˙µƒ¥¥–¬æ´…Ò∫Õ◊€∫œÀÿ÷ .Õı¿œ ¶œÎ≥¢ ‘∏ƒ±‰Ω×ß∑Ω∑®£¨Ω´“‘Õ˘Ωê·—ß…˙◊ˆÃ‚∏ƒŒ™“˝µº—ß…˙ª·—ßœ∞.”⁄ «À˝‘⁄¡‚–Œµƒ—ßœ∞÷–£¨“˝µºÕ¨—ß√«Ω‚戡‚–Œ÷–µƒ“ª∏ˆŒ  ±£¨≤…”√¡À“‘œ¬π˝≥㮫ÎΩ‚æˆÕı¿œ ¶Ã·≥ˆµƒŒ £©£∫
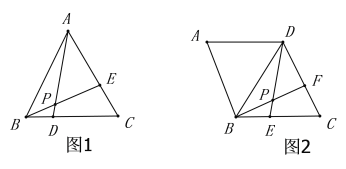
œ»≥ˆ æŒ Ã‚£®1£©:»ÁÕº1£¨‘⁄µ»±þ»˝Ω«–Œ![]() ÷–£¨
÷–£¨![]() Œ™
Œ™![]() …œ“ªµ„£¨
…œ“ªµ„£¨![]() Œ™
Œ™![]() …œ“ªµ„£¨»Áπ˚
…œ“ªµ„£¨»Áπ˚![]() £¨¡¨Ω”
£¨¡¨Ω”![]() °¢
°¢![]() £¨
£¨![]() °¢
°¢![]() œýΩª”⁄µ„
œýΩª”⁄µ„![]() £¨«Û
£¨«Û![]() µƒ∂» ˝.
µƒ∂» ˝.
Õ®π˝—ßœ∞£¨Õı¿œ ¶«ÎÕ¨—ß√«ÀµÀµ◊‘º∫µƒ ’ªÒ.–°√˜Àµ∑¢œ÷“ª∏ˆΩ·¬€£∫‘⁄’‚∏ˆµ»±þ»˝Ω«–Œ![]() ÷–£¨÷ª“™¬˙◊„
÷–£¨÷ª“™¬˙◊„![]() £¨‘Ú
£¨‘Ú![]() µƒ∂» ˝æÕ «“ª∏ˆ∂®÷µ£¨≤ªª·∑¢…˙∏ƒ±‰.ΩÙΩ”◊≈Õı¿œ ¶≥ˆ æ¡ÀŒ £®2£©:»ÁÕº2£¨‘⁄¡‚–Œ
µƒ∂» ˝æÕ «“ª∏ˆ∂®÷µ£¨≤ªª·∑¢…˙∏ƒ±‰.ΩÙΩ”◊≈Õı¿œ ¶≥ˆ æ¡ÀŒ £®2£©:»ÁÕº2£¨‘⁄¡‚–Œ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() Œ™
Œ™![]() …œ“ªµ„£¨
…œ“ªµ„£¨![]() Œ™
Œ™![]() …œ“ªµ„£¨
…œ“ªµ„£¨![]() £¨¡¨Ω”
£¨¡¨Ω”![]() °¢
°¢![]() £¨
£¨![]() °¢
°¢![]() œýΩª”⁄µ„
œýΩª”⁄µ„![]() £¨»Áπ˚
£¨»Áπ˚![]() £¨
£¨![]() £¨«Û≥ˆ¡‚–Œµƒ±þ≥§.
£¨«Û≥ˆ¡‚–Œµƒ±þ≥§.
Œ £®3£©£∫Õ®π˝“‘…œµƒ—ßœ∞«Î–¥≥ˆƒ„µ√µΩµƒ∆٠森“ªÃıº¥ø…£©.
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() £ª£®3£©¥∞∏≤ªŒ®“ª£¨∫œ¿Ìº¥ø…
£ª£®3£©¥∞∏≤ªŒ®“ª£¨∫œ¿Ìº¥ø…
°æΩ‚Œˆ°ø
Œ £®1£©∏˘æð![]() «µ»±þ»˝Ω«–Œ÷§√˜
«µ»±þ»˝Ω«–Œ÷§√˜![]() £¨µ√≥ˆ
£¨µ√≥ˆ![]() £¨‘Ÿ∏˘æð»˝Ω«–ŒÕ‚Ω«–‘÷ º¥ø…µ√÷§£ª
£¨‘Ÿ∏˘æð»˝Ω«–ŒÕ‚Ω«–‘÷ º¥ø…µ√÷§£ª
Œ £®2£©◊˜![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨∏˘æðÀƒ±þ–Œ
£¨∏˘æðÀƒ±þ–Œ![]() «¡‚–Œµ√≥ˆ
«¡‚–Œµ√≥ˆ![]() £¨‘⁄
£¨‘⁄![]() ÷–¿˚”√»˝Ω«∫Ø ˝º¥ø…«Ûµ√
÷–¿˚”√»˝Ω«∫Ø ˝º¥ø…«Ûµ√![]() £¨
£¨![]() £¨◊Ó∫Û∏˘æðπ¥π…∂®¿Ìµ√≥ˆ¥∞∏.
£¨◊Ó∫Û∏˘æðπ¥π…∂®¿Ìµ√≥ˆ¥∞∏.
Œ £®3£©¥”∏ˆ»Àµƒª˝¿€∫Õ–ƒµ√–¥“ªæ‰ª∞º¥ø….
Œ £®1£©°þ![]() «µ»±þ»˝Ω«–Œ£¨
«µ»±þ»˝Ω«–Œ£¨
°ý![]() £¨
£¨![]() .
.
°þ![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() .
.
°þ![]() £¨
£¨
°ý![]() £¨
£¨
Œ £®2£©»ÁÕº£¨◊˜![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨
£¨
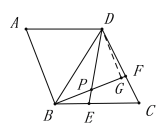
°þÀƒ±þ–Œ![]() «¡‚–Œ£¨
«¡‚–Œ£¨
°ý![]() £¨
£¨![]() £¨
£¨
°ý![]() «µ»±þ»˝Ω«–Œ£¨
«µ»±þ»˝Ω«–Œ£¨
°ý![]() .
.
”…£®1£©ø…÷™![]() £¨
£¨
‘⁄![]() ÷–£¨
÷–£¨
![]() £¨º¥
£¨º¥![]() £¨
£¨
°ý![]() £¨
£¨
![]() £¨º¥
£¨º¥![]() £¨
£¨
°ý![]() .
.
‘⁄![]() ÷–£¨
÷–£¨
”…π¥π…∂®¿Ìø…µ√![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
°ý¡‚–Œµƒ±þ≥§Œ™![]() .
.
Œ £®3£©»Á∆Ω ±”¶∏√◊¢“‚ª˘±æÕº–Œµƒª˝¿€£¨‘⁄—ßœ∞π˝≥Ã÷–◊ˆ∏ˆ”––ƒ»Àµ»£¨—‘÷Æ”–¿Ìº¥ø….



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Àƒ±þ–ŒABCD÷–£¨AB°ŒCD£¨°œB=90°„£¨AB=1£¨CD=2£¨BC=m£¨µ„P «±þBC…œ“ª∂ص„£¨»Ù°˜PAB”ΰ˜PCDœýÀ∆£¨«“¬˙◊„Ãıº˛µƒµ„P«°”–2∏ˆ£¨‘Úmµƒ÷µŒ™_______£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝![]() £Æ
£Æ
£®¢Ò£©“—÷™![]() £¨»Ù∂˛¥Œ∫Ø ˝ÕºœÛ”Î
£¨»Ù∂˛¥Œ∫Ø ˝ÕºœÛ”Î![]() ÷·”–Œ®“ªπ´π≤µ„£¨«Û
÷·”–Œ®“ªπ´π≤µ„£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®¢Ú£©“—÷™![]() £Æ
£Æ
£®¢°£©µ±![]() ±£¨∂˛¥Œ∫Ø ˝ÕºœÛ”Î
±£¨∂˛¥Œ∫Ø ˝ÕºœÛ”Î![]() ÷·”–«“÷ª”–“ª∏ˆπ´π≤µ„£¨«Û
÷·”–«“÷ª”–“ª∏ˆπ´π≤µ„£¨«Û![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®¢¢£©µ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ
”–◊Ó–°÷µ![]() £¨«Û
£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥…ú“‘⁄π∫Ω¯“ªøÓ≤˙∆∑ ±£¨”…”⁄‘À ‰≥…±æº∞≤˙∆∑≥…±æµƒÃ·∏þ£¨∏√≤˙∆∑µ⁄![]() Ãϵƒ≥…±æ
Ãϵƒ≥…±æ![]() £®‘™/º˛£©”Î
£®‘™/º˛£©”Î![]() £®ÃÏ£©÷ƺ‰µƒπÿœµ»ÁÕºÀ˘ 棨≤¢¡¨–¯50ÃÏæ˘“‘80‘™/º˛µƒº€∏Ò≥ˆ €£¨µ⁄
£®ÃÏ£©÷ƺ‰µƒπÿœµ»ÁÕºÀ˘ 棨≤¢¡¨–¯50ÃÏæ˘“‘80‘™/º˛µƒº€∏Ò≥ˆ €£¨µ⁄![]() ÃÏ∏√≤˙∆∑µƒœ˙ €¡ø
ÃÏ∏√≤˙∆∑µƒœ˙ €¡ø![]() £®º˛£©”Î
£®º˛£©”Î![]() £®ÃÏ£©¬˙◊„πÿœµ Ω
£®ÃÏ£©¬˙◊„πÿœµ Ω![]() £Æ
£Æ
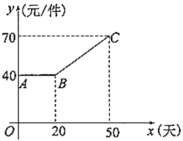
£®1£©µ⁄40ÃÏ£¨∏√…ú“ªÒµ√µƒ¿˚»Û «______‘™£ª
£®2£©…˵⁄![]() ÃÏ∏√…ú“≥ˆ €∏√≤˙∆∑µƒ¿˚»ÛŒ™
ÃÏ∏√…ú“≥ˆ €∏√≤˙∆∑µƒ¿˚»ÛŒ™![]() ‘™£Æ
‘™£Æ
¢Ÿ«Û![]() ”Î
”Î![]() ÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£¨≤¢÷∏≥ˆµ⁄º∏Ãϵƒ¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£¨≤¢÷∏≥ˆµ⁄º∏Ãϵƒ¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
¢⁄‘⁄≥ˆ €∏√≤˙∆∑µƒπ˝≥Ã÷–£¨µ±ÃÏ¿˚»Û≤ªµÕ”⁄1000‘™µƒπ≤”–∂ý…ŸÃÏ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Ω´°˜ABC—ÿ…‰œþBC∆Ω“∆µ√µΩ°˜A°‰B°‰C°‰£¨ πµ√µ„A°‰¬‰‘⁄°œABCµƒ∆Ω∑÷œþBD…œ£¨¡¨Ω”AA°‰£¨AC°‰£Æ
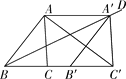
£®1£©≈–∂œÀƒ±þ–ŒABB°‰A°‰µƒ–Œ◊¥£¨≤¢÷§√˜£ª
£®2£©‘⁄°˜ABC÷–£¨AB£Ω6£¨BC£Ω4£¨»ÙAC°‰°ÕA°‰B°‰£¨«ÛÀƒ±þ–ŒABB°‰A°‰µƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬√Ê «–°√˜…˺∆µƒ°∞◊˜»˝Ω«–Œµƒ∏þœþ°±µƒ≥þπÊ◊˜Õºπ˝≥Ã.

“—÷™£∫°˜ABC£Æ
«Û◊˜£∫BC±þ…œµƒ∏þœþ£Æ
◊˜∑®£∫»ÁÕº£¨
¢Ÿ∑÷±“‘A£¨BŒ™‘≤–ƒ£¨¥Û”⁄![]() ≥§Œ™∞Îæ∂ª≠ª°£¨¡Ωª°Ωª”⁄µ„D£¨E£ª
≥§Œ™∞Îæ∂ª≠ª°£¨¡Ωª°Ωª”⁄µ„D£¨E£ª
¢⁄◊˜÷±œþDE£¨”ÎABΩª”⁄µ„F£¨“‘µ„FŒ™‘≤–ƒ£¨FA≥§Œ™∞Îæ∂ª≠‘≤£¨ΩªCBµƒ—”≥§œþ”⁄µ„G£ª
¢€¡¨Ω”AG£Æ
À˘“‘œþ∂ŒAGæÕ «À˘«Û◊˜µƒBC±þ…œµƒ∏þœþ£Æ

∏˘æð–°√˜…˺∆µƒ≥þπÊ◊˜Õºπ˝≥ã¨
£®1£© π”√÷±≥þ∫Õ‘≤πÊ£¨≤π»´Õº–Œ£ª£®±£¡Ù◊˜Õº∫€º££©
£®2£©ÕÍ≥…œ¬√Ê÷§√˜.
÷§√˜£∫¡¨Ω”DA£¨DB£¨EA£¨EB£¨
°þDA=DB£¨
°ýµ„D‘⁄œþ∂ŒABµƒ¥π÷±∆Ω∑÷œþ…œ£® £©£®ÃÓÕ∆¿Ìµƒ“¿æ𣩣Æ
°þ = £¨
°ýµ„E‘⁄œþ∂ŒABµƒ¥π÷±∆Ω∑÷œþ…œ£Æ
°ýDE «œþ∂ŒABµƒ¥π÷±∆Ω∑÷œþ£Æ
°ýFA=FB£Æ
°ýAB «°—Fµƒ÷±æ∂£Æ
°ý°œAGB=90°„£® £©£®ÃÓÕ∆¿Ìµƒ“¿æ𣩣Æ
°ýAG°ÕBC
º¥AGæÕ «BC±þ…œµƒ∏þœþ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨≈◊ŒÔœþy£Ωmx2+2mx©Å3£®m£æ0£©”Îx÷·Ωª”⁄A°¢B¡Ωµ„£®µ„A‘⁄µ„B◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„C£¨∏√≈◊ŒÔœþµƒ∂•µ„Dµƒ◊ð◊¯±Í «©Å4£Æ
£®1£©«Ûµ„A°¢Bµƒ◊¯±Í£ª
£®2£©…Ë÷±œþ”Î÷±œþACπÿ”⁄∏√≈◊ŒÔœþµƒ∂‘≥∆÷·∂‘≥∆£¨«Û÷±œþµƒ±Ì¥Ô Ω£ª
£®3£©∆Ω––”⁄x÷·µƒ÷±œþb”Î≈◊ŒÔœþΩª”⁄µ„M£®x1£¨y1£©°¢N£®x2£¨y2£©£¨”Î÷±œþΩª”⁄µ„P£®x3£¨y3£©£Æ»Ùx1£ºx3£ºx2£¨Ω·∫œ∫Ø ˝ÕºœÛ£¨«Ûx1+x2+x3µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄¡‚–ŒABCD÷–£¨µ„E,F∑÷±‘⁄AB,CD…œ£¨«“![]() £¨¡¨Ω”EFΩªBD”⁄µ„O¡¨Ω”AO.»Ù
£¨¡¨Ω”EFΩªBD”⁄µ„O¡¨Ω”AO.»Ù![]() ,£¨‘Ú
,£¨‘Ú![]() µƒ∂» ˝Œ™£® £©
µƒ∂» ˝Œ™£® £©

A.50°„B.55°„C.65°„D.75°„
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
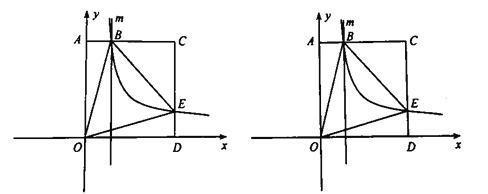
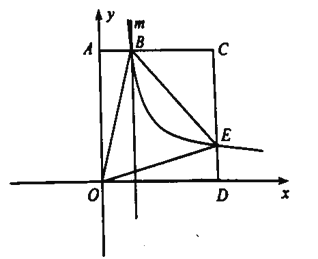
°æƒø°ø»ÁÕº£¨±þ≥§Œ™3’˝∑Ω–Œ![]() µƒ∂•µ„
µƒ∂•µ„![]() ”Α≠µ„÷ÿ∫œ£¨µ„
”Α≠µ„÷ÿ∫œ£¨µ„![]() ‘⁄
‘⁄![]() ÷·£¨
÷·£¨![]() ÷·…œ°£∑¥±»¿˝∫Ø ˝
÷·…œ°£∑¥±»¿˝∫Ø ˝![]() µƒÕºœÛΩª
µƒÕºœÛΩª![]() ”⁄µ„
”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨
£¨![]() .
.
£®1£©«Û∑¥±»¿˝∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©π˝µ„![]() ◊˜
◊˜![]() ÷·µƒ∆Ω––œþ
÷·µƒ∆Ω––œþ![]() £¨µ„
£¨µ„![]() ‘⁄÷±œþ
‘⁄÷±œþ![]() …œ‘À∂Ø£¨µ„
…œ‘À∂Ø£¨µ„![]() ‘⁄
‘⁄![]() ÷·…œ‘À∂Ø.
÷·…œ‘À∂Ø.
¢Ÿ»Ù![]() «“‘
«“‘![]() Œ™÷±Ω«∂•µ„µƒµ»—¸÷±Ω«»˝Ω«–Œ£¨«Û
Œ™÷±Ω«∂•µ„µƒµ»—¸÷±Ω«»˝Ω«–Œ£¨«Û![]() µƒ√ʪ˝£ª
µƒ√ʪ˝£ª
¢⁄Ω´°∞¢Ÿ°±÷–µƒ°∞“‘![]() Œ™÷±Ω«∂•µ„µƒ°±»•µÙ£¨Ω´Œ Â∏ƒŒ™°∞»Ù
Œ™÷±Ω«∂•µ„µƒ°±»•µÙ£¨Ω´Œ Â∏ƒŒ™°∞»Ù![]() «µ»—¸÷±Ω«»˝Ω«–Œ°±£¨
«µ»—¸÷±Ω«»˝Ω«–Œ°±£¨![]() µƒ√ʪ˝≥˝¡À°∞¢Ÿ°±÷–«Ûµ√µƒΩ·π˚Õ‚£¨ªπø…“‘ «______.£®÷±Ω”–¥¥∞∏£¨≤ª”√–¥≤Ω÷Ë£©
µƒ√ʪ˝≥˝¡À°∞¢Ÿ°±÷–«Ûµ√µƒΩ·π˚Õ‚£¨ªπø…“‘ «______.£®÷±Ω”–¥¥∞∏£¨≤ª”√–¥≤Ω÷Ë£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com