
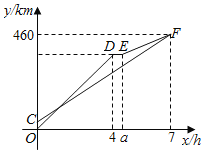
【题目】甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地,甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示
(1)a= ,甲的速度是 km/h;
(2)求线段CF对应的函数表达式,并求乙刚到达货站时,甲距B地还有多远?
(3)乙车出发 min追上甲车?
(4)直接写出甲出发多长时间,甲乙两车相距40km.
【答案】(1)4.5, 60;(2)y=60x+40,180;(3)80;(4)甲出发![]() 小时或
小时或![]() 小时或4小时或7小时后,甲乙两车相距40km.
小时或4小时或7小时后,甲乙两车相距40km.
【解析】
(1)由乙在途中的货站装货耗时半小时易得a=4.5,甲从A到B共用了(![]() +7)小时,然后利用速度公式计算甲的速度;
+7)小时,然后利用速度公式计算甲的速度;
(2)根据甲的速度可求出甲乙出发时甲所走的路程,即可得出线段CF对应的函数表达式;再根据“路程、速度与时间”的关系解答即可;
(3)根据题意列方程求出乙的速度,再列式计算解答即可;
(4)直线OD的解析式为y=90x(0≤x≤4),然后利用函数值相差40列方程解答即可.
(1)∵线段DE代表乙车在途中的货站装货耗时半小时,
∴a=4+0.5=4.5(小时),
甲车的速度=![]() =60(千米/小时);
=60(千米/小时);
故答案为:4.5;60;
(2)乙出发时甲所走的路程为:60×![]() =40(km),
=40(km),
∴线段CF对应的函数表达式为:y=60x+40;
乙刚到达货站时,甲距B地的路程为:460﹣60(4+![]() )=180(km).
)=180(km).
(3)设乙车刚出发时的速度为x千米/时,则装满货后的速度为(x﹣50)千米/时,
根据题意可知:4x+(7﹣4.5)(x﹣50)=460,
解得:x=90.
乙车追上甲车的时间为40÷(90﹣60)=![]() (小时),
(小时),![]() 小时=80分钟,
小时=80分钟,
故答案为:80;
(4)易得直线OD的解析式为y=90x(0≤x≤4),根据题意得
60x+40﹣90x=40或90x﹣(60x+40)=40或60x=460﹣180﹣40或60x=460﹣40,
解得x=![]() 或x=
或x=![]() 或x=4或x=7.
或x=4或x=7.
答:甲出发![]() 小时或x=
小时或x=![]() 小时或x=4小时或x=7小时后,甲乙两车相距40km.
小时或x=4小时或x=7小时后,甲乙两车相距40km.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
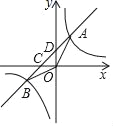
【题目】如图,已知直线y=k1x+b与x轴、y轴相交于C、D两点,与y=![]() 交于A(m,2)、B(﹣2,n)两点.
交于A(m,2)、B(﹣2,n)两点.
(1)求m+n的值;
(2)连接OA、OB,若tan∠AOD+tan∠BOC=1.
①当不等式k1x+b>![]() 时,请结合图象求x的取值范围;
时,请结合图象求x的取值范围;
②设点E在y轴上,且满足∠AEO+∠AOD=45°,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
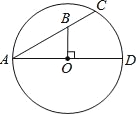
【题目】如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD交AC于点B.若OB=4,则BC长为( )
A. 2 B. 3 C. 3.6 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
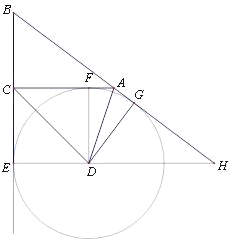
【题目】如图,在△ABC中,BC=a,AC=b,AB=c,⊙D与BC、AC、AB都相切,切点分别是E、F、G,BA、ED的延长线交于点H,a、b是关于x的方程x2﹣(c+4)x+4c+8=0的两个根.
(1)求证:△ABC是直角三角形;
(2)若25asin∠BAC=9c,求四边形CEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() ,有下列说法:
,有下列说法:
①如果当x≤1时![]() 随
随![]() 的增大而减小,则m≥1;
的增大而减小,则m≥1;
②如果它的图象与x轴的两交点的距离是4,则![]() ;
;
③如果将它的图象向左平移3个单位后的函数的最小值是-4,则m=-1;
④如果当x=1时的函数值与x=2013时的函数值相等,则当x=2014时的函数值为-3.
其中正确的说法是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吃香肠是庐江县春节的传统习俗,小严的父亲去年春节前用了![]() 元购买猪肉装香肠;今年下半年受非洲猪瘟影响,猪肉出现大幅度涨价,价格比去年上涨了
元购买猪肉装香肠;今年下半年受非洲猪瘟影响,猪肉出现大幅度涨价,价格比去年上涨了![]() 元
元![]() ,
,
(1)如果去年猪肉价格为![]() 元
元![]() ,求今年
,求今年![]() 元比去年少买多少
元比去年少买多少![]() 猪肉?(结果用
猪肉?(结果用![]() 的式子表示)
的式子表示)
(2)近期县政府为保障猪肉市场供应,为百姓生活着想,采取一系列惠民政策,猪肉价格下降了![]() 元
元![]() ,这样小严的父亲花了
,这样小严的父亲花了![]() 买到和去年一样多的猪肉.求小严父亲今年购买猪肉每千克多少元.
买到和去年一样多的猪肉.求小严父亲今年购买猪肉每千克多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
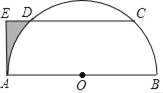
【题目】如图,AB是半圆O的直径,C,D是半圆O上的两点,弧AC=弧BD,AE与弦CD的延长线垂直,垂足为E.
(1)求证:AE与半圆O相切;
(2)若DE=2,AE=![]() ,求图中阴影部分的面积
,求图中阴影部分的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
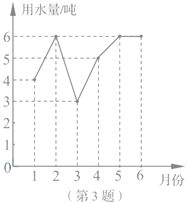
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com