
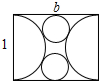
 如图,用邻边分别为1,b(b>1)的矩形硬纸板裁出以1为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥的侧面,小圆恰好作为底面,从而做成两个圆锥(拼接处材料忽略不计),则b的值为( )
如图,用邻边分别为1,b(b>1)的矩形硬纸板裁出以1为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥的侧面,小圆恰好作为底面,从而做成两个圆锥(拼接处材料忽略不计),则b的值为( )| A. | b=$\sqrt{3}$ | B. | b=$\frac{\sqrt{5}+1}{2}$ | C. | b=$\frac{\sqrt{5}}{2}$ | D. | b=$\sqrt{2}$ |
分析 首先利用圆锥形圣诞帽的底面周长等于侧面的弧长求得小圆的半径,然后利用两圆外切的性质得到b的值即可.
解答  解:∵半圆的直径为1,
解:∵半圆的直径为1,
∴半圆的弧长为$\frac{π}{2}$,
∵把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,
∴设小圆的半径为r,则:2πr=$\frac{π}{2}$,
解得:r=$\frac{1}{4}$,
∴AC=$\frac{1}{2}$-r=$\frac{1}{2}$,
如图小圆的圆心为B,半圆的圆心为C,作BA⊥CA于A点,
则:AC2+AB2=BC2
即:($\frac{1}{4}$)2+($\frac{b}{2}$)2=($\frac{1}{2}$+$\frac{1}{4}$)2
整理得:b=$\sqrt{2}$.
故选D.
点评 本题考查了圆锥的计算,解题的关键是利用两圆相外切的性质得到两圆的圆心距,从而利用勾股定理得到b的值.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某公园内有座桥,桥的高度是5米,CB⊥DB,坡面AC的倾斜角为45°,为方便老人过桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,某公园内有座桥,桥的高度是5米,CB⊥DB,坡面AC的倾斜角为45°,为方便老人过桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
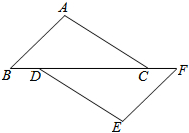 如图,点B、D、C、F在同一直线上,且BD=FC,AB=EF.请你在横线上添加一个条件:∠B=∠ACB(不再添加辅助线),使△ABC≌△EFD,并说明理由.
如图,点B、D、C、F在同一直线上,且BD=FC,AB=EF.请你在横线上添加一个条件:∠B=∠ACB(不再添加辅助线),使△ABC≌△EFD,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
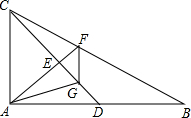 如图,在Rt△ABC中,E为CD的中点,FG∥AC.
如图,在Rt△ABC中,E为CD的中点,FG∥AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-a) | B. | (2,a) | C. | (2,-a) | D. | (a,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com