
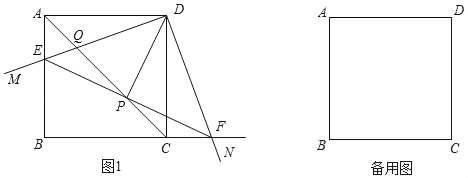
【题目】如图,在正方形ABCD中,边长为4,∠MDN=90°,将∠MDN绕点D旋转,其中DM边分别与射线BA、直线AC交于E、Q两点,DN边与射线BC交于点F;连接EF,且EF与直线AC交于点P.
(1)如图1,点E在线段AB上时,①求证:AE=CF;②求证:DP垂直平分EF;
(2)当AE=1时,求PQ的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)①只要证明△ADE≌△CDE(ASA)即可解决问题;
②利用相似三角形的性质证明∠PDQ=45°即可解决问题;
(2)作QH⊥AD于H,QE⊥AB于G.由△AQD∽△EQP,可知AQPQ=DQEQ,想办法求出AQ,EQ,DQ即可解决问题;
(1)①证明:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=∠DAE=∠DCF=90°,
∴∠ADC=∠MDN=90°,
∴∠ADE=∠CDF,
∴△ADE≌△CDE(ASA),
∴AE=CF.
②∵△ADE≌△CDE(ASA),
∴DE=DF,∵∠MDN=90°,
∴∠DEF=45°,
∵∠DAC=45°,
∴∠DAQ=∠PEQ,∵∠AQD=∠EQP,
∴△AQD∽△EQP,
∴![]() ,
,
∴![]() ,
,
∵∠AQE=∠PQD,
∴△AQE∽△DQP,
∴∠DDP=∠QAE=45°,
∴∠DPE=90°,
∴DP⊥EF,
∵DE=DF,
∴PE=PF,
∴DP垂直平分线段EF.
(2)解:作QH⊥AD于H,QE⊥AB于G.
在Rt△ADE中,DE=![]() ,
,
∵∠QAH=∠QAG=45°,
∴HO=QE=AH=EQ,设QH=x,
∵![]() ×4×x+
×4×x+![]() ×1×x=
×1×x=![]() ×1×4,
×1×4,
∵x=![]() ,
,
∴AQ=![]() ,DQ=
,DQ=![]() =
=![]() ,EQ=
,EQ=![]() ,
,
∵△AQD∽△EQP,
∴AQPQ=DQEQ,
∴PQ=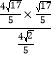 =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是
是![]() 的切线,切点分别为
的切线,切点分别为![]() 、
、![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③若
;③若![]() ,则
,则![]() ;④
;④![]() .其中正确的个数为( )
.其中正确的个数为( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
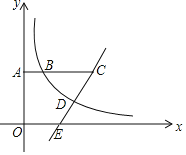
【题目】如图,已知点![]() ,
,![]() ,且点B在双曲线
,且点B在双曲线![]() 上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且
上,在AB的延长线上取一点C,过点C的直线交双曲线于点D,交x轴正半轴于点E,且![]() ,则线段CE长度的取值范围是
,则线段CE长度的取值范围是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,以B为圆心,AB为半径作扇形ABC,交对角线BD于点E,过点E作⊙B的切线分别交AD,CD于G,F两点,则图中阴影部分的面积为( )
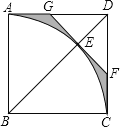
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
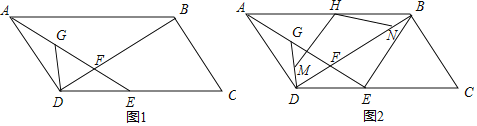
【题目】如图,在平行四边形ABCD中,对角线BD⊥AD,E为CD上一点,连接AE交BD于点F,G为AF的中点,连接DG.
(1)如图1,若DG=DF=1,BF=3,求CD的长;
(2)如图2,连接BE,且BE=AD,∠AEB=90°,M、N分别为DG,BD上的点,且DM=BN,H为AB的中点,连接HM、HN,求证:∠MHN=∠AFB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+5与双曲线![]() (x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是
(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是![]() .若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线
.若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线![]() (x>0)的交点有( )
(x>0)的交点有( )

A. 0个B. 1个C. 2个D. 0个,或1个,或2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,AB⊥BD,CD⊥BD,AP⊥PC,垂足分别为B、P、D,且三个垂足在同一直线上,我们把这样的图形叫“三垂图”.
(1)证明:ABCD=PBPD.
(2)如图乙,也是一个“三垂图”,上述结论成立吗?请说明理由.
(3)已知抛物线与x轴交于点A(-1,0),B(3,0),与y轴交于点(0,-3),顶点为P,如图丙所示,若Q是抛物线上异于A、B、P的点,使得∠QAP=90°,求Q点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
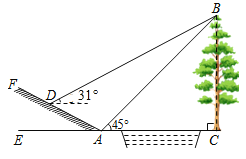
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60).
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60).
(1)求小明从点A走到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com