
分析 (1)直接把点(3,-3)代入反比例函数y=$\frac{k}{x}$,求出k的值即可求得.
(2)把点A(-1,9)B(-3,2)分别代入y=$\frac{k}{x}$,求得k的值,与(1)求得的k比较,即可判断.
解答 解:(1)∵点(3,-3)在反比例函数y=$\frac{k}{x}$的图象上.
∴-3=$\frac{k}{3}$,解得k=-9.
∴这个函数的表达式为y=-$\frac{9}{x}$;
(2)把点A(-1,9)代入y=$\frac{k}{x}$,求得k=-9,
把点B(-3,2)代入y=$\frac{k}{x}$,求得k=-6,
∴点A(-1,9)在这个函数的图象上,点B(-3,2)不在这个函数的图象上.
点评 本题考查的是待定系数法求反比例函数的解析式以及反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:解答题
分别以□ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.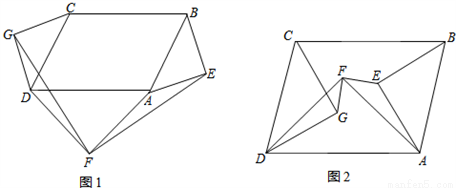
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com