
【题目】如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.

(1)求证:BC=2AB;
(2)若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:
①求点F的运动时间t的值;②求线段AG的长度.
【答案】(1)见解析;(2)①t=3(秒);②AG=![]() .
.
【解析】
(1)先判断出∠DAE=∠AEB,再判断出∠DAE=∠BAE,进而得出∠BAE=∠AEB,即可判断出AB=BE同理:判断出CE=AB,即可得出结论
(2)①先判断出四边形AECF是平行四边形,进而求AF=3,即可得出结论
②先判断出△ABE是等边三角形,进而求出∠AEB=60°,AE=3cm,再判断出∠DCF=∠ECF,即可判断出∠CGE=90°,最后用勾股定理即可得出结论.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠DAE=∠AEB,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
同理:CE=CD,
∴BE=CE=AB,
∴BC=BE+CD=2AB;
(2)①由(1)知,CE=CD=AB,
∵AB=3cm,
∴CE=3cm,
∵四边形ABCD是平行四边形,
∴AD∥BC
∵AE∥CF,
∴四边形AECF是平行四边形,
∴AF=CE=3cm,
∴点F的运动时间t=3÷1=3(秒);
②由(1)知AB=BE,
∵∠B=60°,
∴△ABE是等边三角形,
∴∠AEB=60°,AE=AB=3cm,
∵四边形ABCD是平行四边形,
∴∠B+∠BCD=180°,
∵∠B=60°,
∴∠BCD=120°,
∵AE∥CF,
∴∠ECF=∠AEB=60°,
∴∠DCF=∠BCD﹣∠ECF=60°=∠ECF,
由(1)知,CE=CD=AB=3cm,
∴CF⊥DE,
∴∠CGE=90°,
在Rt△CGE中,∠CEG=90°﹣∠ECF=30°,CG=![]() CE=
CE=![]() ,
,
∴EG=![]() CG=
CG=![]() ,
,
∵∠AEB=60°,∠CEG=30°,
∴∠AEG=90°,
在Rt△AEG中,AE=3,根据勾股定理得,AG=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() ,对角线
,对角线![]() 交于点
交于点![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()

(1)证明:四边形![]() 是平行四边形
是平行四边形
(2)点![]() 是哪些线段的中点,写出结论,并选择一组给出证明.
是哪些线段的中点,写出结论,并选择一组给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值.例:点A、B在数轴上对应的数分别为a、b,则A、B两点间的距离表示为AB=|a﹣b|.根据以上知识解题:
(1)点A在数轴上表示3,点B在数轴上表示2,那么AB=_______.
(2)在数轴上表示数a的点与﹣2的距离是3,那么a=______.
(3)如果数轴上表示数a的点位于﹣4和2之间,那么|a+4|+|a﹣2|=______.
(4)对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值.如果没有.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=![]() cm.
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知![]() ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如![]() 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.

请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”![]() ,必有实数根;
,必有实数根;
(3)若 x 1是“勾系一元二次方程” ![]() 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6![]() ,求ABC 的面积.
,求ABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.

(1)圆心O到CD的距离是______;
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在普通商场中用96元购买了一种商品,后来他在网上发现完全相同的这一商品在网上购买比普通商场中每件少2元,他用90元在网上再次购买这一商品,比上次在普通商场中多买了3件.问小明在网上购买的这一商品每件几元?
查看答案和解析>>
科目:初中数学 来源: 题型:
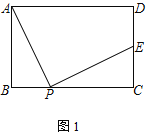
【题目】已知矩形ABCD,点P为边BC上一动点,连接AP,将线段AP绕点P顺时针旋转90°,点A恰好落在直线CD上点E处
(1) 如图1,点E在线段CD上,求证:AD+DE=2AB
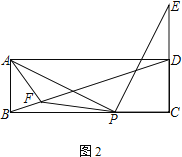
(2) 如图2,点E在线段CD的延长线上,且点D 为线段CE的中点,在线段BD上取点F,连接AF、PF,若AF=AB,求证:∠APF=∠ADB
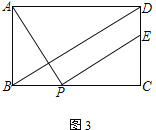
(3) 如图3,点E在线段CD上,连接BD.若AB=2,BD∥PE,则DE=___________ (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
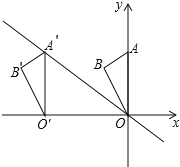
【题目】如图,在平面直角坐标系中点A的坐标为(0,6),点B的坐标为(﹣![]() ,5),将△AOB沿x轴向左平移得到△A′O′B′,点A的对应点A′落在直线y=﹣
,5),将△AOB沿x轴向左平移得到△A′O′B′,点A的对应点A′落在直线y=﹣![]() x上,则点B的对应点B′的坐标为( )
x上,则点B的对应点B′的坐标为( )
A.(﹣8,6)B.(﹣![]() ,5)C.(﹣
,5)C.(﹣![]() ,5)D.(﹣8,5)
,5)D.(﹣8,5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com