
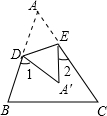
 如图,将∠A=50°的△ABC的∠A沿直线DE折叠,则∠1+∠2=( )
如图,将∠A=50°的△ABC的∠A沿直线DE折叠,则∠1+∠2=( )| A、90° | B、100° |
| C、110° | D、130° |


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
 已知反比例函数y=
已知反比例函数y=| k |
| 2x |
查看答案和解析>>
科目:初中数学 来源: 题型:
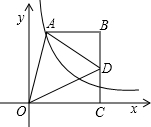 如图,点A在双曲线y=
如图,点A在双曲线y=| k |
| x |
| 5 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
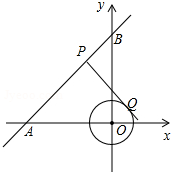 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-4,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-4,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )A、
| ||
B、2
| ||
| C、3 | ||
| D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
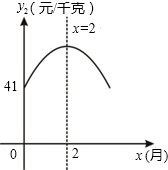 已知:某大型水果种植中心对去年某种时令水果的销售情况统计如下:上半年的销售单价y1(元/千克)与月份x(月)(1≤x≤6,且x为整数)的关系.如下表所示:
已知:某大型水果种植中心对去年某种时令水果的销售情况统计如下:上半年的销售单价y1(元/千克)与月份x(月)(1≤x≤6,且x为整数)的关系.如下表所示:| x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
| y1(元/千克) | 36 | 18 | 12 | 9 | 7.2 | 6 |
| 21 |
| 22 |
| 23 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C).
某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C).查看答案和解析>>
科目:初中数学 来源: 题型:
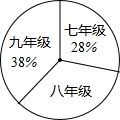 “读书好,读好书,好读书.”阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.为了培养学生的读书习惯,某校组织学生开展“绿色大阅读”活动.右图是在活动之初某校对三个年级学生信息做的一个调查.图1是人数分布扇形统计图,其中八年级人数为408人,表2是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
“读书好,读好书,好读书.”阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.为了培养学生的读书习惯,某校组织学生开展“绿色大阅读”活动.右图是在活动之初某校对三个年级学生信息做的一个调查.图1是人数分布扇形统计图,其中八年级人数为408人,表2是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:| 图书种类 | 频数 | 频率 |
| 科普常识 | 840 | b |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | a | 0.25 |
| 其它 | 144 | 0.06 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com