
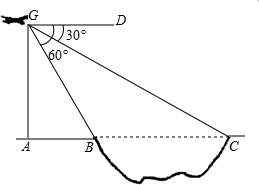
 如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?
如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?| AG |
| GB |
| 900 | ||||
|
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
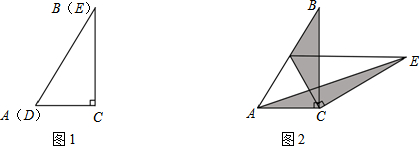
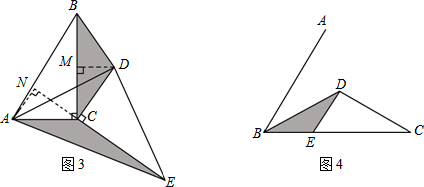
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过B点作PC的垂线,垂足为H.
如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过B点作PC的垂线,垂足为H.查看答案和解析>>
科目:初中数学 来源: 题型:
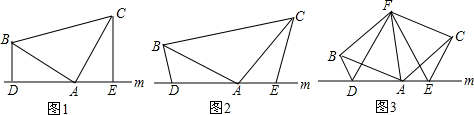
查看答案和解析>>
科目:初中数学 来源: 题型:
|
|
| 252-242 |
| 5a |
| 10b |
1
|
| 3 |
| 1 |
| 2 |
| 10 |
1
|
2
|
1
|
| 2 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与直线都经过坐标轴的正半轴上A(4,0),B两点,该抛物线的对称轴x=-1,与x轴交于点C,且∠ABC=90°,求:
如图,抛物线与直线都经过坐标轴的正半轴上A(4,0),B两点,该抛物线的对称轴x=-1,与x轴交于点C,且∠ABC=90°,求:查看答案和解析>>
科目:初中数学 来源: 题型:
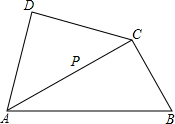 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD的斜边恰好重合已知AB=2,P是AC上的一个动点.
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD的斜边恰好重合已知AB=2,P是AC上的一个动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com