
|

|
|


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
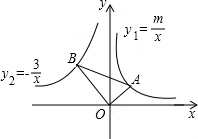 如图,在平面直角坐标系中,∠OAB=60°,∠AOB=90°,反比例函数y1=
如图,在平面直角坐标系中,∠OAB=60°,∠AOB=90°,反比例函数y1=| m |
| x |
| 3 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
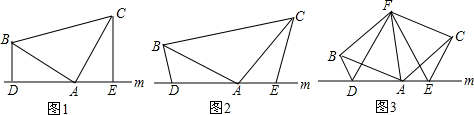
 如图,在长方形ABCD中,将△ABC沿AC对折至△AEC位置,CE与AD交于点F.
如图,在长方形ABCD中,将△ABC沿AC对折至△AEC位置,CE与AD交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
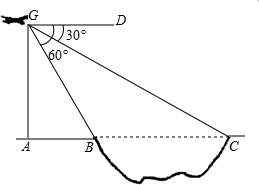 如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?
如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com