
分析 (1)根据平方差公式,可得答案;
(2)根据分母有理化,可得答案;
(3)根据分母有理化,可得平方差公式,根据平方差公式,可得答案.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;
(2)$\sqrt{11}$-$\sqrt{10}$=$\frac{1}{\sqrt{11}+\sqrt{10}}$,$\sqrt{12}$-$\sqrt{11}$=$\frac{1}{\sqrt{12}+\sqrt{11}}$,
$\sqrt{11}$-$\sqrt{10}$>$\sqrt{12}$-$\sqrt{11}$;
(3)原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2016}$-$\sqrt{2015}$)($\sqrt{2016}$+1)
=($\sqrt{2016}$-1)($\sqrt{2016}$+1)
=2016-1
=2015.
点评 本题考查了分母有理化,利用平方差公式是分母有理化的关键.


科目:初中数学 来源: 题型:解答题
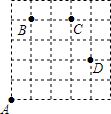 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A→B(+1,+4),从D到C记为:D→C(-1,+2),其中第一个数表示左右方向,第二个数表示上下方向.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A→B(+1,+4),从D到C记为:D→C(-1,+2),其中第一个数表示左右方向,第二个数表示上下方向.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
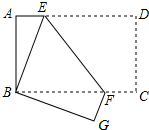 如图,将长方形纸片ABCD折叠,使点D与B重合,点C落到G处,折痕为EF,若∠ABE=20°,则∠EFG的度数为( )
如图,将长方形纸片ABCD折叠,使点D与B重合,点C落到G处,折痕为EF,若∠ABE=20°,则∠EFG的度数为( )| A. | 125° | B. | 120° | C. | 135° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,一只蚂蚁在正方体的一个顶点A处,它能爬到顶点B处寻找食物,若这个正方体的边长为1,则这只蚂蚁所爬行的最短路程为( )
如图所示,一只蚂蚁在正方体的一个顶点A处,它能爬到顶点B处寻找食物,若这个正方体的边长为1,则这只蚂蚁所爬行的最短路程为( )| A. | 8 | B. | $\sqrt{2}+1$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
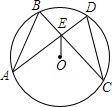 如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知$\widehat{AB}$=$\widehat{CD}$.
如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知$\widehat{AB}$=$\widehat{CD}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com