
 ��֪����x��һԪ���η���x2$+2x+\frac{k-1}{2}=0$����������ȵ�ʵ������kΪ��������
��֪����x��һԪ���η���x2$+2x+\frac{k-1}{2}=0$����������ȵ�ʵ������kΪ������������ ��1������һԪ���η��̸����б�ʽ��ȷ����k�ķ�Χ�����kΪ��������������⣻
��2������һԪ���η��̵�һ����Ϊ0��ȷ����k������$\left\{\begin{array}{l}{y={x}^{2}+2x}\\{y=x+2}\end{array}\right.$ȷ�����������꣬�����MN��m�ĺ�����ϵʽ�����ɣ�
��3������ͼ����ص㣬������������ۣ��ֱ����b��ֵ���ɣ�
��4�����ݵ�A��M��N�����꣬ȷ����AM��AN��MN���жϳ��������������������Σ�
��� �⣺��1������x��һԪ���η���x2$+2x+\frac{k-1}{2}=0$����������ȵ�ʵ������
���=b2-4ac=4-4��$\frac{k-1}{2}$��0��k-1��2��
���k��3��
��k��������
��k=1��2��
��2����ͼ1��
��x=0ʱ��$\frac{k-1}{2}$=0�����k=1��
��k=1ʱ�����κ���Ϊy=x2+2x��
������������ֱ�ߣ���
$\left\{\begin{array}{l}{y={x}^{2}+2x}\\{y=x+2}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$����A��-2��0����B��1��3����
��M��m��m+2��������-2��m��1��N��m��m2+2m����
MN=m+2-��m2+2m��=-m2-m+2=-��m+$\frac{1}{2}$��2+$\frac{9}{4}$��
��m=-$\frac{1}{2}$ʱ��MN���=$\frac{9}{4}$����ʱM��-$\frac{1}{2}$��$\frac{3}{2}$����
��3���ٵ�ֱ��y=$\frac{1}{2}$x+b��A��ʱ��ֱ��y=$\frac{1}{2}x$+b�����ͼ��ǡ�������������㣬��ͼ2��
��A��������룬��$\frac{1}{2}$����-2��+b=0��
���b=1��
�ڵ�y=$\frac{1}{2}$x+b����ͼ��ķ�ղ�����һ��������ʱ��ֱ������ͼ����3�������㣬
������ͼ��ķ�ղ�����ԭͼ��ķ�ղ��ֹ���x��Գƣ����������ʽΪy=-x2-2x
��$\left\{\begin{array}{l}{y=\frac{1}{2}x+b}\\{y=-{x}^{2}-2x}\end{array}\right.$��һ���
��-x2-$\frac{5}{2}$x-b=0��������ȵ�ʵ������
��-$\frac{5}{2}$��2-4����-1������-b��=0��
���b=$\frac{25}{16}$��
����������ֱ��y=$\frac{1}{2}x$+b�����ͼ��ǡ�������������㣬��ʱb��ֵΪ1��$\frac{25}{16}$��
��4�����ɣ�2���У�A��-2��0����M��-$\frac{1}{2}$��$\frac{3}{2}$����N��-$\frac{1}{2}$��-$\frac{3}{4}$����
��MN=$\frac{9}{4}$��AM=$\frac{3\sqrt{2}}{2}$��AN=$\frac{3\sqrt{5}}{4}$��
��MN��AM��AN��û����ȵ��߶Σ�
��ƽ�����ݣ������ڵ�P��ʹ��M��N��A��PΪ������ı���Ϊ���Σ�
���� �����Ƕ��κ����ۺ����ͣ���Ҫ�����˸����б�ʽ��Ӧ�ã���������������ͼ��Ľ������⣬�ѵ����ڣ�3�����ֱ������������3��������������������������ۣ���������ͼ�θ����ڽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
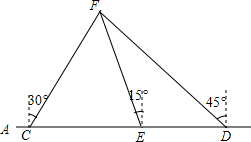 ��ͼ���ڶ�������ĺ�����AB�ϣ���C��D����Ѳ�ߴ����־��յ����ϴ�F������źţ���֪C��D�������50��$\sqrt{2}$+$\sqrt{6}$�������F�ڴ�C�ı�ƫ��30�㷽���ϣ���F�ڴ�D�����������ϣ�������AB����һ�۲��E����ô�F�����ڹ۲��E�ı�ƫ��15�㷽���ϣ�
��ͼ���ڶ�������ĺ�����AB�ϣ���C��D����Ѳ�ߴ����־��յ����ϴ�F������źţ���֪C��D�������50��$\sqrt{2}$+$\sqrt{6}$�������F�ڴ�C�ı�ƫ��30�㷽���ϣ���F�ڴ�D�����������ϣ�������AB����һ�۲��E����ô�F�����ڹ۲��E�ı�ƫ��15�㷽���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
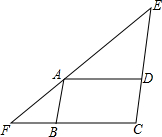 ��ͼ���ڡ�EFC�У���A��EF��һ�㣬��AD��CF��AB��CE����EAD=��BAF��
��ͼ���ڡ�EFC�У���A��EF��һ�㣬��AD��CF��AB��CE����EAD=��BAF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\sqrt{5}$ | B�� | -2 | C�� | 2 | D�� | $\sqrt{5}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com