

分析 (1)利用平方法比较大小(两个都是非负数)即可;
(2)由于a,b为非负数,利用作差法先比较它们的平方,再结合a2≥0,即可;
(3)利用射影定理,直角三角形斜边的中线等于斜边的一半;
(4)利用梯形的面积公式和前面得到的结论,即可.
解答 解:(1)①∵(2+3)2=25,(2$\sqrt{2×3}$)=4×6=24,
而25>24,
∴2+3>2$\sqrt{2×3}$,
②∵(3+$\frac{1}{4}$)2=$\frac{169}{16}$,(2$\sqrt{3×\frac{1}{4}}$)2=3,
而$\frac{169}{16}$>3,
∴3+$\frac{1}{4}$>$\sqrt{3×\frac{1}{4}}$,
③∵8+8=16,2$\sqrt{8×8}$=2×8=16,
∴8+8=2$\sqrt{8×8}$;
故答案为>,>,=;
(2)∵对任意的非负实数a,b,
∴(a+b)2-(2$\sqrt{ab}$)2=a2+b2+2ab-4ab=a2+b2-2ab=(a-b)2;
∵(a-b)2≥0,
∴(a+b)2-(2$\sqrt{ab}$)2≥0,
∴a+b≥2$\sqrt{ab}$;
(3)根据射影定理得到:CD2=AD×BD,
∵AD=2a,BD=2b,
∴CD2=4ab,
∴CD=2$\sqrt{ab}$,
∵CO是Rt△ABC斜边上的中线,
∴OC=$\frac{1}{2}$(AD+BD)=$\frac{1}{2}$(2a+2b)=a+b,
Ⅰ、当直角三角形不为等腰直角三角形时,
∵OC是Rt△OCD斜边,
∴OC>CD,
∴a+b>2$\sqrt{ab}$
Ⅱ、当直角三角形是等腰直角三角形时,点C,D重合,
∴OC=CD,
∴a+b=2$\sqrt{ab}$
即:OC≥CD,
∴a+b≥2$\sqrt{ab}$;
故答案为a+b≥2$\sqrt{ab}$(当a=b时,取等号);
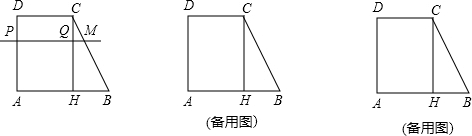
(4)设EG=a,FH=b,
根据梯形面积公式得,ab=7200,
∵a+b≥2$\sqrt{ab}$=2$\sqrt{7200}$=120$\sqrt{2}$,
∴a+b的最小值为60$\sqrt{2}$,
∴包装带至少需要2(a+b)=2×120$\sqrt{2}$=240$\sqrt{2}$cm.
点评 此题是四边形综合题,主要考查了比较无理数大小的一种方法(针对两个非负数,平方大的它也大),射影定理,直角三角形斜边的中线等于斜边的一半,用平方法比较无理数大小的方法是解本题的关键,用几何图形证明结论是本题的难点.


科目:初中数学 来源: 题型:选择题
| A. | 1.239×10-3 | B. | 1.2×10-3 | C. | 1.239×10-2 | D. | 1.239×10-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根,k为正整数.
已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根,k为正整数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
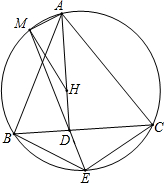 如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.
如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
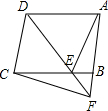 如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证:
如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com