Question

13．[问题提出]
学习了等腰三角形的性质和特殊四边形的性质和判定方法后，书本上有这样一个习题，要求证明等腰三角形底边上的一点到两腰的距离和为定值，我们继续对“等腰三角形底边延长线上的一点到腰的距离与腰的关系”进行研究．
[初步思考]我们不妨将问题用符号语言表示为：已知如图，在等腰△ABC中，AB=AC，然后分点D在BC上，点D在BC的延长线上，点D在CB的延长线上三种情况进行研究．
[深入探究]
第一种情况：
若点D是底边BC上的任意一点，DE⊥AB于点E，DF⊥AC于点F，求证：DE+DF等于一腰上的高．
第二种情况：
若点D是底边CB延长线上的任意一点，DE⊥AB交AB的延长线于点E，DF⊥AC于点F，DE+DF还为定值吗？如果不为定值，探究DE，DF与等腰三角形一腰上的高的关系．
第三种情况：
若点D是底边BC延长线上的任意一点，DE⊥AB于点E，DF⊥AC交AC的延长线于点F，DE+DF还为定值吗？如果不为定值，探究DE，DF与等腰三角形一腰上的高的关系．
[结论]根据你探究的结果，你能归纳出等腰三角形的一个性质吗？

Answer 1

分析 第一种情况：连接AD，根据三角形的面积公式即可得到$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$AC•BG，根据等腰三角形的性质进而求得DE+DF=BG；
第二种情况：过B作BM⊥FD，垂足为M，易证四边形BGFM是矩形，利用AAS可证△DBM≌△DBE，那么DM=DE，易证DF-DE=CG；
第三种情况：过C作CM⊥ED，垂足为M，易证四边形CGEM是矩形，利用AAS可证△DCM≌△DCF，那么DM=DF，易证DE-DF=CG．

解答 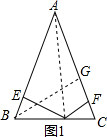解：第一种情况：
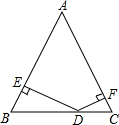
如图1，连接AD，过B作BG⊥AC与G，
∴S_△ABC=$\frac{1}{2}$AC×BG，
∵S_△ABD=$\frac{1}{2}$AB•DE，S_△ADC=$\frac{1}{2}$AC•DF，
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$AC•BG，
∵AB=AC，
∴$\frac{1}{2}$AB（DE+DF）=$\frac{1}{2}$AB•AC，
∴DE+DF=BG；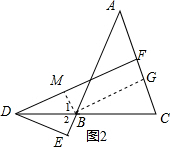
第二种情况：DF-DE=CG．
证明：如图3所示，过B作BG⊥AC与G，过B作BM⊥ED，垂足为M，
∵DF⊥AC，
∴∠CMD=∠CFD=90°，
∵AB=AC，
∴∠ABC=∠ACB，
∵∠ABC=∠EBD，
∴∠C=∠EBD，
∵DE⊥AB，BM⊥DF，
∴BM∥AC，
∴∠C=∠MBD，
∴∠MBD=∠EBD，
在△BMD和△BED中，
$\left\{\begin{array}{l}{∠BMD=∠E}\\{∠MBD=∠EBD}\\{BD=BD}\end{array}\right.$，
∴△BMD≌△BED（AAS），
∴DM=DE，
∵四边形GBMF为长方形，
∴BG=FM，
∵FM+MD=DF，
∴BG+DE=DF，
即DF-DE=CG；
第三种情况：DE-DF=CG．
证明：如图3所示，过C作CG⊥AB与G，过C作CM⊥ED，垂足为M，
∵DF⊥AC，
∴∠CMD=∠CFD=90°，
∵AB=AC，
∴∠B=∠ACB，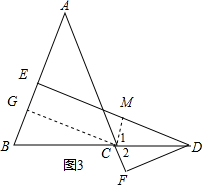
∵∠ACB=∠FCD，
∴∠B=∠FCD，
∵DE⊥AB，CM⊥DE，
∴CM∥AB，
∴∠B=∠MCD，
∴∠MCD=∠FCD，
在△CMD和△CFD中，
$\left\{\begin{array}{l}{∠CMD=∠CFD}\\{∠MCD=∠FCD}\\{CD=CD}\end{array}\right.$，
∴△CMD≌△CFD（AAS），
∴DM=DF，
∵四边形GCME为长方形，
∴CG=EM，
∵EM+MD=DE，
∴CG+DF=DE，
即DE-DF=CG．

点评 本题考查了全等三角形的判定与性质及等腰三角形的性质；辅助线的作出是正确解答本题的关键．