
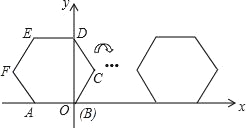
【题目】已知边长为2的正六边形ABCDEF在平面直角坐标系中的位置如图所示,点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2018次翻转之后,点B的坐标是______.
【答案】(4033,![]() )
)
【解析】
根据正六边形的特点,每6次翻转为一个循环组循环,用2018除以6,根据商和余数的情况确定出点B的位置,经过第2017次翻转之后,点B的位置不变,仍在x轴上,由A(﹣2,0),可得AB=2,即可求得点B离原点的距离为4032,所以经过2017次翻转之后,点B的坐标是(4032,0),经过2018次翻转之后,点B在B′位置(如图所示),则△BB′C为等边三角形,可求得BN=NC=1,B′N=![]() ,由此即可求得经过2018次翻转之后点B的坐标.
,由此即可求得经过2018次翻转之后点B的坐标.
然后求出翻转前进的距离,过点C作CG⊥x于G,求出∠CBG=60°,然后求出CG、BG,再求出OG,然后写出点C的坐标即可.
设2018次翻转之后,在B′点位置,
∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,
∴每6次翻转为一个循环组,
∵2018÷6=336余2,
∴经过2016次翻转为第336个循环,点B在初始状态时的位置,
而第2017次翻转之后,点B的位置不变,仍在x轴上,
∵A(﹣2,0),
∴AB=2,
∴点B离原点的距离=2×2016=4032,
∴经过2017次翻转之后,点B的坐标是(4032,0),
经过2018次翻转之后,点B在B′位置,则△BB′C为等边三角形,
此时BN=NC=1,B′N=![]() ,
,
故经过2018次翻转之后,点B的坐标是:(4033,![]() ).
).
故答案为:(4033,![]() ).
).


科目:初中数学 来源: 题型:
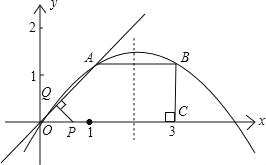
【题目】如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C、A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
(1)求经过O、A、B三点的抛物线解析式;
(2)求S与t的函数关系式;
(3)将△OPQ绕着点P顺时针旋转90°,是否存在t,使得△OPQ的顶点O或Q在抛物线上?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;
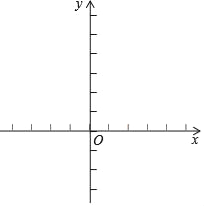
查看答案和解析>>
科目:初中数学 来源: 题型:
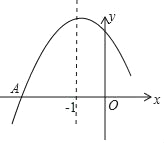
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若B(﹣![]() ,y1),C(﹣
,y1),C(﹣![]() ,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④
,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④![]() <0,其中正确的结论是_____.
<0,其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+x+2
x2+x+2![]() 与x轴交于A,B两点,交y轴于点C,点C关于抛物线对称轴对称的点为D.
与x轴交于A,B两点,交y轴于点C,点C关于抛物线对称轴对称的点为D.
(1)求点D的坐标及直线AD的解析式;
(2)如图1,连接CD、AD、BD,点M为线段CD上一动点,过M作MN∥BD交线段AD于N点,点P是y轴上的动点,当△CMN的面积最大时,求△MPN的周长取得最小值时点P的坐标;
(3)如图2,线段AE在第一象限内交BD于点E,其中tan∠EAB=![]() ,将抛物线向右水平移动,点A平移后的对应点为点G;将△ABD绕点B逆时针旋转,旋转后的三角形纪为△A1BD1,若射线BD1与线段AE的交点为F,连接FG.若线段FG把△ABF分成△AFG和△BFG两个三角形,是否存在点G,使得△AFG是直角三角形且△BFG是等腰三角形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
,将抛物线向右水平移动,点A平移后的对应点为点G;将△ABD绕点B逆时针旋转,旋转后的三角形纪为△A1BD1,若射线BD1与线段AE的交点为F,连接FG.若线段FG把△ABF分成△AFG和△BFG两个三角形,是否存在点G,使得△AFG是直角三角形且△BFG是等腰三角形?若存在,请直接写出点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,AB⊥x轴于C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.

(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)在x轴上存在一点P,使S△AOP= ![]() S△AOB, 求点P的坐标.
S△AOB, 求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并回答问题.事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方,这个结论就是著名的勾股定理.请利用这个结论,完成下面活动:
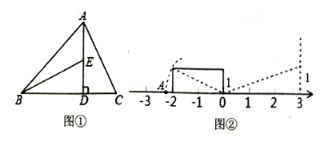
![]() 一个直角三角形的两条直角边分别为
一个直角三角形的两条直角边分别为![]() ,那么这个直角三角形斜边长为____;
,那么这个直角三角形斜边长为____;
![]() 如图①,
如图①,![]() 于
于![]() ,求
,求![]() 的长度;
的长度;
![]() 如图②,点
如图②,点![]() 在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数
在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数![]() 的
的![]() 点(保留痕迹).
点(保留痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,点
,点![]() 将线段
将线段![]() 分成两部分,如果
分成两部分,如果![]() ,那么称点
,那么称点![]() 为线段
为线段![]() 的黄金分割点.
的黄金分割点.
![]() 某研究小组在进行课题学习时,类似地给出“黄金分割线”的定义:直线
某研究小组在进行课题学习时,类似地给出“黄金分割线”的定义:直线![]() 将一个面积为
将一个面积为![]() 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为![]() ,
,![]() ,如果
,如果![]() ,那么称直线
,那么称直线![]() 为该图形的黄金分割线.(如图
为该图形的黄金分割线.(如图![]() )
)
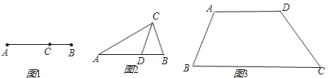
问题.试在图![]() 的梯形中画出至少五条黄金分割线,并说明理由.
的梯形中画出至少五条黄金分割线,并说明理由.
![]() 类似“黄金分割线”得“黄金分割面”定义:截面
类似“黄金分割线”得“黄金分割面”定义:截面![]() 将一个体积为
将一个体积为![]() 的图形分成体积为V1
的图形分成体积为V1
、![]() 的两个图形,且
的两个图形,且![]() ,则称直线
,则称直线![]() 为该图形的黄金分割面.
为该图形的黄金分割面.
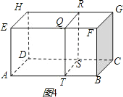
问题:如图![]() ,长方体
,长方体![]() 中,
中,![]() 是线段
是线段![]() 上的黄金分割点,证明经过
上的黄金分割点,证明经过![]() 点且平行于平面
点且平行于平面![]() 的截面
的截面![]() 是长方体的黄金分割面.
是长方体的黄金分割面.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com