
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若B(﹣![]() ,y1),C(﹣
,y1),C(﹣![]() ,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④
,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④![]() <0,其中正确的结论是_____.
<0,其中正确的结论是_____.
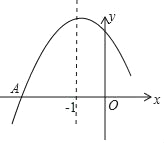
【答案】①③
【解析】
①由抛物线交y轴于正半轴可得出c>0,结论①正确;②由点B,C的横坐标可得出点C离对称轴远,结合抛物线开口向下,即可得出y1>y2,结论②错误;③由抛物线的对称轴为直线x=-1,可得出b=2a,即2a-b=0,结论③正确;④由抛物线顶点的纵坐标大于0,可得出![]() >0,结论④错误.综上即可得出结论.
>0,结论④错误.综上即可得出结论.
①∵抛物线交y轴于正半轴,
∴c>0,结论①正确;
②∵抛物线的对称轴为直线x=-1,
∴-1-(-![]() )<-
)<-![]() -(-1).
-(-1).
又∵抛物线的开口向下,B(-![]() ,y1),C(-
,y1),C(-![]() ,y2)为图象上的两点,
,y2)为图象上的两点,
∴y1>y2,结论②错误;
③∵抛物线的对称轴为直线x=-1,
∴-![]() =-1,
=-1,
∴b=2a,即2a-b=0,结论③正确;
④∵抛物线的顶点纵坐标在x轴上方,
∴![]() >0,结论④错误.
>0,结论④错误.
故答案为:①③.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为D,对称轴为直线x=1,有下列四个判断:
①关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=﹣1,x2=3;
②a﹣b+c=0;
③若抛物线上有三个点分别为(﹣2,y1)、(1,y2)、(2,y3),则y1<y2<y3;
④当OC=3时,点P为抛物线对称轴上的一个动点,则△PCA的周长的最小值是![]() ,
,
上述四个判断中正确的 有( )
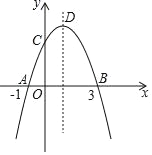
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科研小组获取了声音在空气中传播的速度v与空气温度t关系的一些数据如下表:
温度t(°C) | -20 | -10 | 0 | 10 | 20 | 30 |
声速v(m/s) | 318 | 324 | 330 | 336 | 342 | 348 |
(1)根据表中提供的信息,可推测速度v是温度t的一次函数,请你写出其函数表达式;
(2)当空气温度为25°C,声音10秒可以传播多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】企业的污水处理有两种方式:一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1至6月,该企业向污水厂输送的污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间满足的函数关系如下表:
月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
输送的污水量y1(吨) | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
7至12月,该企业自身处理的污水量y2(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为y2=ax2+c(a≠0).其图象如图所示.1至6月,污水厂处理每吨污水的费用:z1(元)与月份x之间满足函数关系式:z1=![]() x,该企业自身处理每吨污水的费用:z2(元)与月份x之间满足函数关系式:z2=
x,该企业自身处理每吨污水的费用:z2(元)与月份x之间满足函数关系式:z2=![]() x﹣
x﹣![]() x2;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
x2;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
(1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识,分别直接写出y1,y2与x之间的函数关系式;
(2)请你求出该企业去年哪个月用于污水处理的费用W(元)最多,并求出这个最多费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为2的正六边形ABCDEF在平面直角坐标系中的位置如图所示,点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2018次翻转之后,点B的坐标是______.
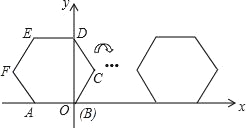
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD的对角线交于点O,已知△OBC的周长为59厘米,且AD的长是28厘米,两对角线的差为14厘米,那么较长的一条对角线长是______厘米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)若D(2,3),请在网格图中画一个格点△DEF,使△DEF ∽△ABC,且相似比为2∶1;
(2)求∠D的正弦值;
(3)若△ABC外接圆的圆心为P,则点P的坐标为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com