
����Ŀ����ҵ����ˮ���������ַ�ʽ��һ�������͵���ˮ�����м��д�������һ����ͨ����ҵ�������豸���д�����ij��ҵȥ��ÿ�µ���ˮ����Ϊ12000�֣�������ˮ�����ڵ��ԽΣ���ˮ�����������ޣ�����ҵͶ���Խ��豸������ˮ�����ִ�����ʽͬʱ���У�1��6�£�����ҵ����ˮ�����͵���ˮ��y1���֣����·�x��1��x��6����xȡ������֮������ĺ�����ϵ���±���
���·�x���£� | ��1 | ��2 | 3 | ��4 | 5 | 6 |
�����͵���ˮ��y1���֣� | ��12000 | ��6000 | ��4000 | ��3000 | ��2400 | 2000 |
7��12�£�����ҵ������������ˮ��y2���֣����·�x��7��x��12����xȡ������֮��������κ�����ϵʽΪy2=ax2+c��a��0������ͼ����ͼ��ʾ��1��6�£���ˮ������ÿ����ˮ�ķ��ã�z1��Ԫ�����·�x֮�����㺯����ϵʽ��z1=![]() x������ҵ��������ÿ����ˮ�ķ��ã�z2��Ԫ�����·�x֮�����㺯����ϵʽ��z2=
x������ҵ��������ÿ����ˮ�ķ��ã�z2��Ԫ�����·�x֮�����㺯����ϵʽ��z2=![]() x��
x��![]() x2��7��12�£���ˮ������ÿ����ˮ�ķ��þ�Ϊ2Ԫ������ҵ��������ÿ����ˮ�ķ��þ�Ϊ1.5Ԫ��
x2��7��12�£���ˮ������ÿ����ˮ�ķ��þ�Ϊ2Ԫ������ҵ��������ÿ����ˮ�ķ��þ�Ϊ1.5Ԫ��
��1����۲����еı����ͼ������ѧ����һ�κ�������������������κ������й�֪ʶ���ֱ�ֱ��д��y1��y2��x֮��ĺ�����ϵʽ��
��2�������������ҵȥ���ĸ���������ˮ�����ķ���W��Ԫ����࣬�������������ã�

���𰸡���1��y1=![]() ��1��x��6����xȡ��������y2=x2+10000��7��x��12����xȡ����������2��ȥ��5��������ˮ�����ķ�����࣬��������22000Ԫ��
��1��x��6����xȡ��������y2=x2+10000��7��x��12����xȡ����������2��ȥ��5��������ˮ�����ķ�����࣬��������22000Ԫ��
��������
��1�����ñ��������ݿ��Եó�xy=��ֵ����y1��x֮��ĺ�����ϵΪ������������ϵ������ɣ������ú���ͼ��ó���ͼ�����7��10049������12��10144���㣬�������ʽ���ɣ���2�����õ�1��x��6ʱ���Լ���7��x��12ʱ���ֱ����������ˮ�ķ��ã����������
��1�����ݱ��������ݿ��Եó�xy=��ֵ����y1��x֮��ĺ�����ϵΪ������������ϵ��
y1=![]() ������1��12000������ã�
������1��12000������ã�
k=1��12000=12000��
��y1=![]() ��1��x��6����xȡ��������
��1��x��6����xȡ��������
����ͼ����Եó���ͼ�����7��10049������12��10144���㣬
����y2=ax2+c��a��0���ã�![]() ��
��
��ã�![]() ��
��
��y2=x2+10000��7��x��12����xȡ��������
��2����1��x��6����xȡ����ʱ��
W=y1z1+��12000��y1��z2=![]()
![]() x+��12000��
x+��12000��![]() ����
����![]() x��
x��![]() x2����
x2����
=��1000x2+10000x��3000��
��a=��1000��0��x=��![]() =5��1��x��6��
=5��1��x��6��
�൱x=5ʱ��W���=22000��Ԫ����
��7��x��12ʱ����xȡ����ʱ��
W=2����12000��y2��+1.5y2=2����12000��x2��10000��+1.5��x2+10000����
=��![]() x2+19000��
x2+19000��
��a=��![]() ��0��x=��
��0��x=��![]() =0��
=0��
��7��x��12ʱ��W��x���������С��
�൱x=7ʱ��W���=18975.5��Ԫ����
��22000��18975.5��
��ȥ��5��������ˮ�����ķ�����࣬��������22000Ԫ��


 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
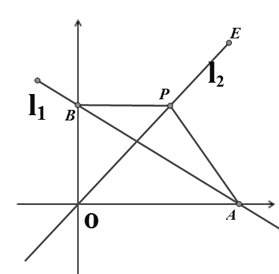
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ��
��![]() ����
����![]() ������
������![]() ��
��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() .
.
��1����ֱ��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2����ֱ��![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() �������ڣ������
�������ڣ������![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
��3����![]() ��
��![]() ���ϵ�һ�����㣬��
���ϵ�һ�����㣬��![]() ��
��![]() ���ϵ�һ�����㣬����
���ϵ�һ�����㣬����![]() ��
��![]() ��Ĵ��߽�ֱ��
��Ĵ��߽�ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() �ǵ���ֱ�������Σ���ֱ��д������������
�ǵ���ֱ�������Σ���ֱ��д������������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ž���ֽƬABCD�۵���ʹ��������A��C�غϣ��ۺ�ΪFG����AB��4��BC��8��
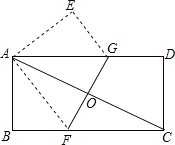
��1���߶�BF�ij���
��2���ж���AGF��״��֤����
��3�����߶�GF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
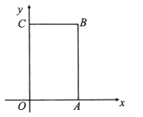
����Ŀ����ͼ��������OABC�У�OΪƽ��ֱ������ϵ��ԭ�㣬A�������Ϊ(4��0)��C�������Ϊ(0��6)����B�ڵ�һ�����ڣ���P��ԭ���������ÿ��2����λ���ٶ�����O��A��B��C��O��·���ƶ��ڵ�P�ƶ������У���P�㵽x��ľ���Ϊ5����λʱ����P�ƶ���ʱ��Ϊ________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
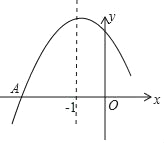
����Ŀ����ͼ�Ƕ��κ���y��ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊֱ��x����1�������ĸ����ۣ���c��0������B����![]() ��y1����C����
��y1����C����![]() ��y2��Ϊͼ���ϵ����㣬��y1��y2����2a��b��0����
��y2��Ϊͼ���ϵ����㣬��y1��y2����2a��b��0����![]() ��0��������ȷ�Ľ�����_____��
��0��������ȷ�Ľ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���2x2+2x��1=0��������Ϊx1��x2����x1��x2�����н�����ȷ���ǣ�������
A. x1+x2=1 B. x1x2=��1 C. |x1|��|x2| D. x12+x1=![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA��OB��AB��x����C����A��![]() ��1���ڷ���������y=
��1���ڷ���������y=![]() ��ͼ���ϣ�
��ͼ���ϣ�

��1����������y=![]() �ı���ʽ��
�ı���ʽ��
��2����x���ϴ���һ��P��ʹS��AOP= ![]() S��AOB�� ���P�����꣮
S��AOB�� ���P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С������������Ϊ1��ֽ�������������һ�������ǽ�С�Ľ���Ϊ60�㣬�������ص����ֵ����Ϊ��������

A. 3 B. 2 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90�㣬AC=6cm��BC=8cm����D�ӵ�C��������2 cm/s ���ٶ�������C��A��B���B�˶���ͬʱ��E�ӵ�B��������1 cm/s���ٶ���BC�����C�˶������E�˶���ʱ��Ϊt ����λ��s����0��t��8��.
(1) ����BDE ��ֱ��������ʱ����t��ֵ��
(2)���ı���CDEF����CD��DEΪһ���ڱߵ�ƽ���ı��Σ������������ΪS����S����t�ĺ�����ϵʽ�����Ƿ����ij��ʱ��t��ʹƽ���ı���CDEFΪ����?�����ڣ����t��ֵ���������ڣ���˵������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com