
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为D,对称轴为直线x=1,有下列四个判断:
①关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=﹣1,x2=3;
②a﹣b+c=0;
③若抛物线上有三个点分别为(﹣2,y1)、(1,y2)、(2,y3),则y1<y2<y3;
④当OC=3时,点P为抛物线对称轴上的一个动点,则△PCA的周长的最小值是![]() ,
,
上述四个判断中正确的 有( )
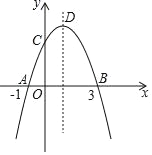
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
由抛物线与对称轴的交点对①进行判断;由抛物线经过点(-1,0),代入解析式即可对②进行判断;利用抛物线的对称轴对③进行判断;利用抛物线的对称性得到PA=PB,当B、P、C在一条直线上时,PB+PC=BC,此时PA+PC最小,则△PCA的周长最小,根据勾股定理求得AC、BC即可对④进行判断.
∵抛物线y=ax2+bx+c与x轴交于点A(-1,0)、B(3,0),
∴关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=-1,x2=3,故①正确;
∵抛物线y=ax2+bx+c与x轴交于点A(-1,0),
∴a-b+c=0,故②正确;
∵抛物线开口向下,对称轴为直线x=![]() =1,抛物线上有三个点分别为(-2,y1)、(1,y2)、(2,y3),
=1,抛物线上有三个点分别为(-2,y1)、(1,y2)、(2,y3),
∴|-2-1|>|2-1|,
∴y1<y3<y2,故③错误;
∵P为抛物线对称轴上的一个动点,
∴点A与点B为抛物线的对称点,
∴PA=PB,
∴PA+PC=PB+PC,
当B、P、C在一条直线上时,PB+PC=BC,
此时PA+PC最小,则△PCA的周长最小,
∵OA=1,OC=3,OB=3
∴AC=![]() ,BC=2
,BC=2![]() ,
,
∴△PCA的周长最小值为![]() +2
+2![]() .故④错误.
.故④错误.
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中正确的结论有( )
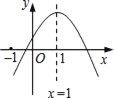
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸片ABCD折叠,使两个顶点A、C重合,折痕为FG,若AB=4,BC=8.
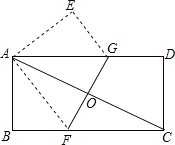
求(1)线段BF的长;
(2)判断△AGF形状并证明;
(3)求线段GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;
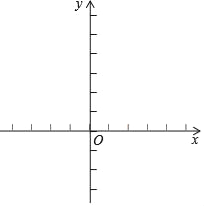
查看答案和解析>>
科目:初中数学 来源: 题型:
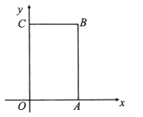
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位的速度沿着O→A→B→C→O的路线移动在点P移动过程中,当P点到x轴的距离为5个单位时,点P移动的时间为________
查看答案和解析>>
科目:初中数学 来源: 题型:
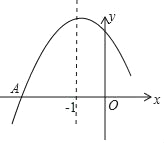
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若B(﹣![]() ,y1),C(﹣
,y1),C(﹣![]() ,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④
,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④![]() <0,其中正确的结论是_____.
<0,其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,AB⊥x轴于C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.

(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)在x轴上存在一点P,使S△AOP= ![]() S△AOB, 求点P的坐标.
S△AOB, 求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com