
【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动。若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求: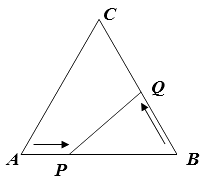
(1)经过6秒后,BP= cm,BQ=cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于 ![]() cm2 ?
cm2 ?
【答案】
(1)6;12
(2)
∵△ABC是等边三角形,
∴AB=AC=12cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,
∴∠BPQ=30°,
∴BP=2BQ
∵BP=12-x,BQ=2x,
∴12-x=2×2x,
∴ ![]()
当∠QPB=90°时,
∴∠PQB=30°,
∴BQ=2PB,
∴2x=2(12-x),
x=6
答:6秒或 ![]() 秒时,△BPQ是直角三角形;
秒时,△BPQ是直角三角形;
(3)
作QD⊥AB于D,
∴∠QDB=90°,
∴∠DQB=30°,
∴DB =0.5 BQ=x,
在Rt△DBQ中,由勾股定理,得
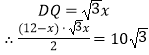
解得;x1=10,x2=2,
∵x=10时,2x>12,故舍去
∴x=2.
答:经过2秒△BPQ的面积等于 ![]() cm2
cm2
【解析】(1)解:由题意,得
AP=6cm,BQ=12cm.
∵△ABC是等边三角形
∴AB=BC=12cm,
∴BP=12-6=6cm.
【考点精析】根据题目的已知条件,利用等边三角形的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】小红的妈妈买了4筐白菜,以每筐25千克为标准,超过的千克数记为正数,不足的千克数记为负数,称重后的记录分别为+0.25,-1, +0.5, 0.75。小红快速准确地算出了4筐白菜的总质量为( )
A. 一1千克 B. 1千克 C. 99千克 D. 101千克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为( ).
A. 4,4,8,8 B. 5,5,7,7 C. 5.5,5.5,6.5,6.5 D. 3,3,9,9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=x+2与y=-2x+6的图象相交于点A,函数y=-2x+6的图象分别交x轴、y轴于点B、C,函数y=x+2的图象分别与x轴、y轴交于点E、D.
(1)求点A的坐标;
(2)求△ABE的面积.
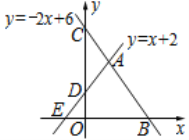
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张勤同学的父母在外打工,家中只有年迈多病的奶奶.星期天早上,李老师从家中出发步行前往张勤家家访.6分钟后,张勤从家出发骑车到相距1200米的药店给奶奶买药,停留14分钟后以相同的速度按原路返回,结果与李老师同时到家.张勤家、李老师家、药店都在东西方向笔直大路上,且药店在张勤家与李老师家之间.在此过程中设李老师出发t(0≤t≤32)分钟后师生二人离张勤家的距离分别为S1、S2 . S1与t之间的函数关系如图所示,请你解答下列问题: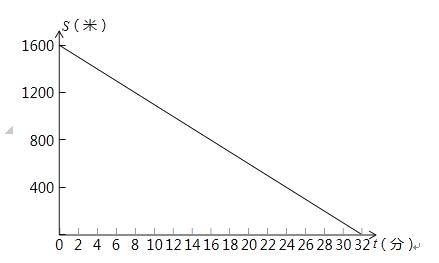
(1)李老师步行的速度为。
(2)求S2与t之间的函数关系式,并在如图所示的直角坐标系中画出其函数图象;
(3)张勤出发多长时间后在途中与李老师相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com