
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=![]() ,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是_____.
,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是_____.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=∠C,点D在BC上,点E在AC上,连接DE且∠ADE=∠AED
(1)若∠B=70°,∠ADE=80°,求∠BAD,∠CDE.
(2)当点D在BC(点B,C除外)边上运动时,且点E在AC边上,猜想∠BAD与∠CDE的数量关系是,并证明你的猜想.

(3)当点D在BC(点B,C除外)边上运动时,且点E在AC边上,若∠BAD=25°,求∠CDE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣x+a(a>0),当自变量x取m时,其相应的函数值小于0,那么下列结论中正确的是( )
A.m﹣1>0
B.m﹣1<0
C.m﹣1=0
D.m﹣1与0的大小关系不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一次函数y=(a+1)x+(a﹣4)的图象不经过第二象限,且关于x的分式方程![]() 有整数解,那么整数a值不可能是( )
有整数解,那么整数a值不可能是( )
A. 0B. 1C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(2)班组织了一次朗读比赛,甲、乙两队各10人的比赛成绩(10分制)如下表(单位:分):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算乙队成绩的平均数和方差;
(3)已知甲队成绩的方差是1.4分2 , 则成绩较为整齐的是队.
查看答案和解析>>
科目:初中数学 来源: 题型:
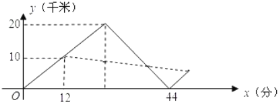
【题目】2018年5月,某城遭遇暴雨水灾,武警战士乘一冲锋舟从A地逆流而上,前往C地营救受困群众,途经B地时,由所携带的救生艇将B地受困群众运回A地,冲锋舟继续前进,到C地接到群众后立刻返回A地,途中曾与救生艇相遇,冲锋舟和救生艇距A地的距离y(千米)和冲锋舟出发后所用时间x(分)之间的函数图象如图所示,假设群众上下冲锋舟和救生艇的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(1)冲锋舟从A地到C地的时间为 分钟,冲锋舟在静水中的速度为 千米/分,水流的速度为 千米/分.
(2)冲锋舟将C地群众安全送到A地后,又立即去接应救生艇,已知救生艇与A地的距离y(千米)和冲锋舟出发后所用时间x(分钟)之间的函数关系式为y=kx+b,若冲锋舟在距离A地![]() 千米处与救生艇第二次相遇,求k、b的值.
千米处与救生艇第二次相遇,求k、b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中, ![]() ,点D在BC所在的直线上,点E在射线AC上,且
,点D在BC所在的直线上,点E在射线AC上,且![]() ,连接DE.
,连接DE.
(1)如图①,若![]() ,
, ![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,若![]() ,
, ![]() ,求
,求![]() 的度数;
的度数;
(3)当点D在直线BC上(不与点B、C重合)运动时,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com