
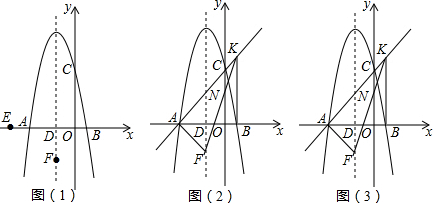
分析 (1)由抛物线的截距为5得出C点坐标及OC长度,由OC=5OB得出B点坐标,将B点坐标代入抛物线解析式得到一个a与b的方程,再根据对称轴为-2得到另一个a与b的方程,两个方程联立解出a、b即可;
(2)△HEP是以HE为斜边的等腰直角三角形时,可证△HLP≌△PME,HL=PM,EM=LP,设出M点横坐标m,则L、H、的坐标均可用m表示,HL、ML的长度可以用m表示,根据HL+EM=ML列出方程解之即可;
(3)分两种情况:第一种,翻折之后,F点落在AK下方,设GF'与NK交于点R,由面积关系推出GNF'K是平行四边形;第二种,翻折之后,F点落在AK上方,设NF'与AK交于点R,由面积积推出GNKF'是平行四边形.
解答 解:(1)
对于抛物线y=ax2+bx+5(a≠0),
令x=0,则y=5,
∴C(0,5),
∵OC=5OB,
∴B(1,0),
∵F(-2,-3)在抛物线对称轴上,
∴$-\frac{b}{2a}$=-2,
∴b=4a,
将B(1,0)代入y=ax2+bx+5(a≠0)可得a+b+5=0,
∴a=-1,b=-4,
∴抛物线的解析式为y=-x2-4x+5;
(2)如图(1)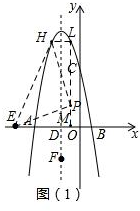
∵△EPH是等腰直角三角形,
∴PH=HE,∠EPH=90°,
∴∠HPL+∠EPM=90°,
∵∠EPM+∠PEM=90°,
∴∠PEM=HPL,
∴△EPL≌△PEM,
∴HL=PM,ME=PL,
设M(m,0),则L(m,-m2-4m+5),H(-4-m,-m2-4m+5)
∴HL=PM=2m+4,PL=EM=m+7,
∴2m+4+m+7=-m2-4m+5,
解得:m=-1或m=-6(舍去),
∴PM=HL=2,
∴P(-1,2);
(3)令-x2-4x+5=0,得x=-5或x=1,
∴A(-5,0),B(1,0)
∴AC的解析式为:y=-x+5,
∴K(1,6),
FK=$\sqrt{[1-(-2)]^{2}+[6-(-3)]^{2}}=3\sqrt{10}$,
①若翻折后,点F'在直线AK下方,记F'G与KN交于点R,连接F'K,如图(2),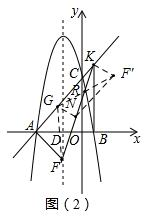
∴${S}_{△GNR}=\frac{1}{4}{S}_{△FGK}=\frac{1}{2}{S}_{△GNK}$=$\frac{1}{2}{S}_{△GNF'}$,
即:S△GNR=S△F'NR=S△KGR,
∴NR=KR,GR=F'R,
∴F'KGN是平行四边形,
∴KG=F'N=FN=$\frac{1}{2}KF=\frac{3\sqrt{10}}{2}$;
(3)②若翻折后,点F'在直线AK上方,记F'N与GK交点R,连接F'K,如图(3),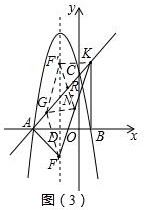
∴${S}_{△GNR}=\frac{1}{4}{S}_{△FGK}=\frac{1}{2}{S}_{△GNK}$=$\frac{1}{2}{S}_{△GNF'}$,
即:S△GNR=S△F′GR=S△KNR,
∴GR=RK,NR=F'R,
∴F'GNK是平行四边形,
∴FG=F'G=KN=$\frac{1}{2}$KF=$\frac{3\sqrt{10}}{2}$,
∵A(-5,0),F(-2,-3),
∴∠FAO=45°,AF=3$\sqrt{2}$,
∵∠CA0=45°,
∴AF⊥AK,
∴AG=$\sqrt{F{G}^{2}-A{F}^{2}}$=$\frac{3}{2}\sqrt{2}$,
∴KG=KA-AG=$\frac{9}{2}\sqrt{2}$;
综上所述,KG=$\frac{3\sqrt{10}}{2}$或KG=$\frac{9\sqrt{2}}{2}$.
点评 本题考查了待定系数法求二次函数解析式,全等三角形的判定与性质、一元二次方程的解法、勾股定理、平行四边形的判定与性质,等面积变换、翻折变换等知识点,难度较大,是一道经典压轴题.(2)问当通过证明△EPL≌△PEM得出线段相等关系是解决问题的关键;(3)问当中,注意要分两种情况讨论,每种情况当中,通过面积和相等变换得出GNF'K或GNKF'是平行四边形是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
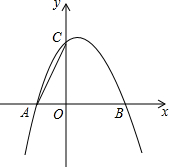 如图,二次函数y=-x2+bx+c的图象与x轴交于点A(-1,0),B(2,0),与y轴相交于点C.
如图,二次函数y=-x2+bx+c的图象与x轴交于点A(-1,0),B(2,0),与y轴相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
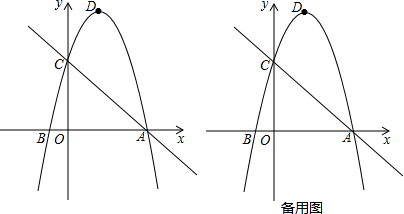
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
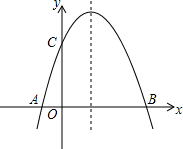 已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧,与y轴交于点C,点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.
已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧,与y轴交于点C,点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
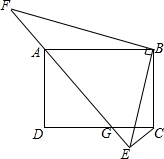 如图,在矩形ABCD中,AB=4,BC=3,G是CD边上的动点(点G不与点C、D重合),CE⊥AG的延长线于G点,BF⊥BE交EA的延长线于F点.
如图,在矩形ABCD中,AB=4,BC=3,G是CD边上的动点(点G不与点C、D重合),CE⊥AG的延长线于G点,BF⊥BE交EA的延长线于F点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com