
 ��ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx-2��a��0����x�ύ��A��1��0����B��3��0�����㣬��y�ύ�ڵ�C���䶥��Ϊ��D����E������Ϊ��0��-1��������������BE������һ��F������BC��
��ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx-2��a��0����x�ύ��A��1��0����B��3��0�����㣬��y�ύ�ڵ�C���䶥��Ϊ��D����E������Ϊ��0��-1��������������BE������һ��F������BC������ ��1���ô���ϵ������������߽���ʽ��
��2�������M���ù��ɶ��������M�����꣬�Ӷ����MD��������ʱ��t��
��3���ɡ�PBF��BAƽ�֣�ȷ��������B��ֱ��BN�Ľ���ʽ�������ֱ�ߺ������ߵĽ��㼴�ɣ�
��� �⣺��1����������y=ax2+bx-2��a��0����x�ύ��A��1��0����B��3��0�����㣬
��$\left\{\begin{array}{l}{a+b-2=0}\\{9a+3b-2=0}\end{array}\right.$��
��$\left\{\begin{array}{l}{a=-\\;\frac{2}{3}}\\{b=\frac{8}{3}}\end{array}\right.$��
�������߽���ʽΪy=-$\frac{2}{3}$x2+$\frac{8}{3}$x-2��
��2����ͼ1��
�ɣ�1��֪y=-$\frac{2}{3}$x2+$\frac{8}{3}$x-2=-$\frac{2}{3}$��x-2��2+$\frac{2}{3}$��
��DΪ�����ߵĶ��㣬
��D��2��$\frac{2}{3}$����
��һ����M�ӵ�D��������ÿ��1����λ���ٶ�ƽ������y�᷽�������˶���
����M��2��m������m��$\frac{2}{3}$����
��OM2=m2+4��BM2=m2+1��OB2=9��
�ߡ�OMB=90�㣬
��OM2+BM2=OB2��
��m2+4+m2+1=9��
��m=$\sqrt{2}$��m=-$\sqrt{2}$���ᣩ��
��M��0��$\sqrt{2}$����
��MD=$\sqrt{2}$-$\frac{2}{3}$��
��һ����M�ӵ�D��������ÿ��1����λ���ٶ�ƽ������y�᷽�������˶���
��t=$\sqrt{2}$-$\frac{2}{3}$��
��3�����ڵ�P��ʹ��PBF��BAƽ�֣�
��ͼ2��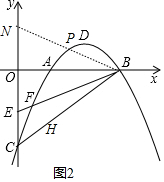
���PBO=��EBO��
��E��0��-1����
����y����ȡһ��N��0��1����
��B��3��0����
��ֱ��BN�Ľ���ʽΪy=-$\frac{1}{3}$x+1�٣�
�ߵ�P��������y=-$\frac{2}{3}$x2+$\frac{8}{3}$x-2���ϣ�
�����٢ڵ�$\left\{\begin{array}{l}{y=-\frac{1}{3}x+1}\\{y=-\frac{2}{3}{x}^{2}+\frac{8}{3}x-2}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=\frac{3}{2}\\;}\\{y=\frac{1}{2}}\end{array}\right.$�� $\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$����ȥ����
��P��$\frac{3}{2}$��$\frac{1}{2}$����
���� ���⿼����κ����ۺ��⡢����ϵ������һ�κ�����Ӧ�á������ε������ƽ���ߵ�֪ʶ������ʱ�������������ѧ֪ʶ��ѧ�ṹ��һ�κ��������÷����������������Ľ������꣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
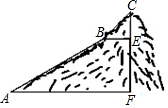 ��ͼ��Ϊ����һ��ɽ��CF�ĸ߶ȣ�����ɽ��ij��ɽ�»���ΪAB��BC���Σ�ÿһ��ɽ�½����ǡ�ֱ���ģ����в���³�AB=600�ף�BC=200�ף��½ǡ�BAF=30�㣬��CBE=45�㣮������������ţ�
��ͼ��Ϊ����һ��ɽ��CF�ĸ߶ȣ�����ɽ��ij��ɽ�»���ΪAB��BC���Σ�ÿһ��ɽ�½����ǡ�ֱ���ģ����в���³�AB=600�ף�BC=200�ף��½ǡ�BAF=30�㣬��CBE=45�㣮������������ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
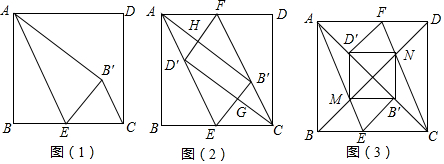
 ���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ���2a+b=0����a+c��b����������y=ax2+bx+c��x�����һ������Ϊ��3��0������abc��0��������ȷ�Ľ����Ǣ٢ܣ���д��ţ�
���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ���2a+b=0����a+c��b����������y=ax2+bx+c��x�����һ������Ϊ��3��0������abc��0��������ȷ�Ľ����Ǣ٢ܣ���д��ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
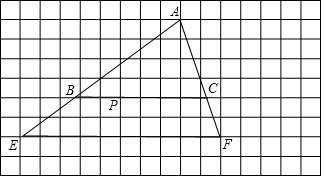
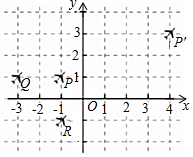 ��ͼ��ʾ�����ܷɻ�P��Q��R���ֱ�ӷ��У�ijʱ��������ϵ�е�����ֱ�Ϊ��-1��1������-3��1������-1��-1����30��ɻ�P�ɵ�P�䣨4��3��λ�ã���ɻ�Q��R��λ��Q�䣬R��ֱ�Ϊ��������
��ͼ��ʾ�����ܷɻ�P��Q��R���ֱ�ӷ��У�ijʱ��������ϵ�е�����ֱ�Ϊ��-1��1������-3��1������-1��-1����30��ɻ�P�ɵ�P�䣨4��3��λ�ã���ɻ�Q��R��λ��Q�䣬R��ֱ�Ϊ��������| A�� | Q�䣨2��3����R�䣨4��1�� | B�� | Q�䣨2��3����R�䣨2��1�� | C�� | Q�䣨2��2����R�䣨4��1�� | D�� | Q�䣨3��3����R�䣨3��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com