
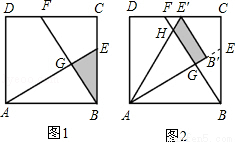
(12分)如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1,∠BAE=30°.

(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB'E'(如图2),使点E落在CD边上的点E'处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
(1)证明见试题解析;(2)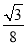 ;(3)没有变化,理由见试题解析.
;(3)没有变化,理由见试题解析.
【解析】
试题分析:(1)由四边形ABCD是正方形,可得∠ABE=∠BCF=90°,AB=BC,又由AE⊥BF,由同角的余角相等,即可证得∠BAE=∠CBF,然后利用ASA,即可判定:△ABE≌△BCF;
(2)由正方形ABCD的面积等于3,即可求得此正方形的边长,由在△BGE与△ABE中,∠GBE=∠BAE,∠EGB=∠EBA=90°,可证得△BGE∽△ABE,由相似三角形的面积比等于相似比的平方,即可求得答案;
(3)易证得Rt△ABE≌Rt△AB′E′≌Rt△ADE′,可得AB′与AE在同一直线上,即BF与AB′的交点是G,然后设BF与AE′的交点为H,可证得△BAG≌△HAG,继而证得结论.
试题解析:(1)∵四边形ABCD是正方形,∴∠ABE=∠BCF=90°,AB=BC,∴∠ABF+∠CBF=90°,
∵AE⊥BF,∴∠ABF+∠BAE=90°,∴∠BAE=∠CBF,
在△ABE和△BCF中,∵∠ABE=∠BCF,AB=BC,∠BAE=∠CBF,∴△ABE≌△BCF.
(2)【解析】
∵正方形面积为3,∴AB=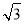 ,
,
在△BGE与△ABE中,∵∠GBE=∠BAE,∠EGB=∠EBA=90°,∴△BGE∽△ABE,
∴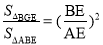 ,
,
又∵BE=1,∴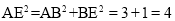 ,∴S△BGE=
,∴S△BGE=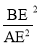 ×S△ABE=
×S△ABE=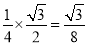 ;
;
(3)【解析】
没有变化.
理由:∵AB=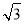 ,∠BAE=30°,∴BE=1,
,∠BAE=30°,∴BE=1,
∵AB′=AB=AD,∠AB′E′=∠ADE'=90°,AE′公共,
∴Rt△ABE≌Rt△AB′E′≌Rt△ADE′,
∴∠DAE′=∠B′AE′=∠BAE=30°,
∴AB′与AE在同一直线上,即BF与AB′的交点是G,
设BF与AE′的交点为H,
则∠BAG=∠HAG=30°,而∠AGB=∠AGH=90°,AG公共,
∴△BAG≌△HAG,
∴S四边形GHE′B′=S△ABE′﹣S△AGH=S△ABE﹣S△ABG=S△BGE.
∴△ABE在旋转前后与△BCF重叠部分的面积没有变化.
考点:1.相似三角形的判定与性质;2.全等三角形的判定与性质;3.正方形的性质.


科目:初中数学 来源:2014-2015学年辽宁省大石桥市水源镇二九年级上学期期末模拟检测数学试卷(解析版) 题型:解答题
(8分)如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)C(-2,-5):

(1)在图中作出△ABC关于y轴对称的图形△A1B1C1;并写出A1、B1、C1点的坐标。
(2)在图中作出△ABC关于原点对称的图形△A2B2C2;并写出A2、B2、C2点的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省庄河市七年级上学期期中考试数学试卷(解析版) 题型:选择题
我国最长的河流长江全长约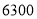 千米,用科学计数法表示为( )
千米,用科学计数法表示为( )
A.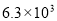 千米 B.
千米 B.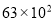 千米 C.
千米 C.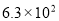 千米 D.
千米 D.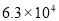 千米
千米
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省庄河市八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,点A、E、F、C在同一直线上, AD∥BC, AD=BC, AE=CF. 求证: BE=DF

查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省庄河市八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图, AD⊥BC, D是BC边的中点, 下面结论: (1)△ADB≌△ADC; (2)△ABC是等腰三角形; (3)∠B=∠C; (4)AD是∠BAC的平分线, 其中正确的是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省庄河市七年级上学期期中考试数学试卷(解析版) 题型:解答题
庄河开往大连的火车上原有(6a-2b)人,中途下车一半人,又上车若干人,使车上共有乘客(10a-6b)人,问上车的乘客是多少人?当a=100, b=80时,上车的乘客是多少人?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省锦州市七年级上学期期中考试数学试卷(解析版) 题型:填空题
据中新社报道:2010年我国粮食产量将达到540 000 000 000 kg,用科学记数法表示这个粮食产量为 kg.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com