
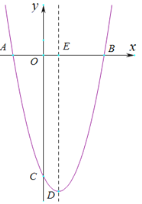
【题目】如图,抛物线y=ax-2x+c(a≠0)与x轴,y轴分别交于点A,B,C三点,已知点(-2,0),C(0,-8),点D是抛物线的顶点.
(1)求抛物线的解析式及顶点D的坐标;
(2)如图,抛物线的对称轴与x轴交于点E,第四象限的抛物线上有一点P,将△EB直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,求点P的坐标;
【答案】(1)y=x2﹣2x﹣8;D(1,﹣9);(2)P(![]() ,
,![]() ).
).
【解析】
(1)将点A、点C的坐标代入抛物线的解析式可求得a、c的值,从而得到抛物线的解析式,最后利用配方法可求得点D的坐标;
(2)将y=0代入抛物线的解析式求得点B的坐标,然后由抛物线的对称轴方程可求得点E的坐标,由折叠的性质可求得∠BEP=45°,设直线EP的解析式为y=-x+b,将点E的坐标代入可求得b的值,从而可求得直线EP的解析式,最后将直线EP的解析式和抛物线的解析式联立组成方程组求解即可.
解:(1)将点A、点C的坐标代入抛物线的解析式得:![]() ,
,
解得:a=1,c=﹣8.
∴抛物线的解析式为y=x2﹣2x﹣8.
∵y=(x﹣1)2﹣9,
∴D(1,﹣9).
(2)将y=0代入抛物线的解析式得:x2﹣2x﹣8=0,解得x=4或x=﹣2,
∴B(4,0).
∵y=(x﹣1)2﹣9,
∴抛物线的对称轴为x=1,
∴E(1,0).
∵将△EBP沿直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,
∴EP为∠BEF的角平分线.
∴∠BEP=45°.
设直线EP的解析式为y=﹣x+b,将点E的坐标代入得:﹣1+b=0,解得b=1,
∴直线EP的解析式为y=﹣x+1.
将y=﹣x+1代入抛物线的解析式得:﹣x+1=x2﹣2x﹣8,解得:x=![]() 或x=
或x=![]() .
.
∵点P在第四象限,
∴x=![]() .
.
∴y=![]() .
.
∴P(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+b与x轴相交于点A,与y轴相交于点B,抛物线y=ax2﹣4ax+4经过点A和点B,并与x轴相交于另一点C,对称轴与x轴相交于点 D.
x+b与x轴相交于点A,与y轴相交于点B,抛物线y=ax2﹣4ax+4经过点A和点B,并与x轴相交于另一点C,对称轴与x轴相交于点 D.
(1)求抛物线的表达式;
(2)求证:△BOD∽△AOB;
(3)如果点P在线段AB上,且∠BCP=∠DBO,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在斜坡上按水平距离间隔50米架设电缆,塔柱上固定电缆的位置![]() ,
,![]() 离塔柱底部的距离均为20米.若以点
离塔柱底部的距离均为20米.若以点![]() 为原点,以水平地面
为原点,以水平地面![]() 所在的直线为
所在的直线为![]() 轴,建立如图所示的坐标系,已知斜坡
轴,建立如图所示的坐标系,已知斜坡![]() 所在直线的解析式为
所在直线的解析式为![]() ,两端挂起的电缆下垂近似成二次项系数
,两端挂起的电缆下垂近似成二次项系数![]() 为抛物线的形状.
为抛物线的形状.
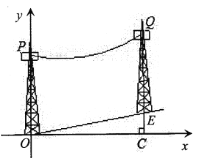
(1)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;
的坐标为 ;
(2)求电缆近似成的抛物线的解析式;
(3)小明说:在抛物线顶点处,下垂的电缆在竖直方向上与斜坡的距离最近。你是否认同?请计算说明。
查看答案和解析>>
科目:初中数学 来源: 题型:
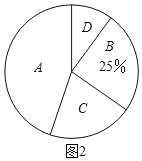
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践室及创客空间,致力于从小培养孩子的创新精神和创造能力,郑州市某校开设了“3D”打印、数学编程、智能机器人、陶艺制作”四门创客课程,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查(问卷调查表如表所示),将调查结果整理后绘制成图1、图2两幅均不完整的统计图表.
图1
创客课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
最受欢理的创客课程词查问卷
你好!这是一份关于你喜欢的创客深程问卷调查表,请你在表格中选择一个(只能选择一个)你最喜欢的课程选项在其后空格内打“√“,非常感谢你的合作.
选项 | 创客课程 | |
A | “3D”打印 | |
B | 数学编程 | |
C | 智能机器人 | |
D | 陶艺制作 |
请根据图表中提供的值息回答下列问题:
(1)统计表中的a= .b= ;
(2)“D”对应扇形的圆心角为 ;
(3)根据调查结果,请你估计该校2000名学生中最喜欢“数学编程”创客课程的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
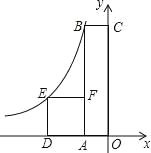
【题目】如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=![]() (k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为( )
(k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为( )
A. 4B. -4C. 6D. -6
查看答案和解析>>
科目:初中数学 来源: 题型:
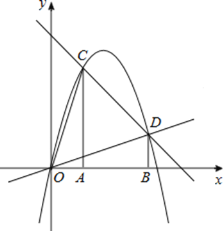
【题目】如图,过![]() 、
、![]() 作x轴的垂线,分别交直线
作x轴的垂线,分别交直线![]() 于C、D两点
于C、D两点![]() 抛物线
抛物线![]() 经过O、C、D三点.
经过O、C、D三点.
![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
![]() 若
若![]() 沿CD方向平移
沿CD方向平移![]() 点C在线段CD上,且不与点D重合
点C在线段CD上,且不与点D重合![]() ,在平移的过程中
,在平移的过程中![]() 与
与![]() 重叠部分的面积记为S,试求S的最大值.
重叠部分的面积记为S,试求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场批发甲、乙两种水果,根据以往经验和市场行情,预计夏季某一段时间内,甲种水果的销售利润y甲(万元)与进货量x(吨)近似满足函数关系y甲=0.3x;乙种水果的销售利润y乙(万元)与进货量x(吨)近似满足函数关系y乙=ax2+bx(其中a≠0,a,b为常数),且进货量x为1吨时,销售利润y乙为1.4万元;进货量x为2吨时,销售利润y乙为2.6万元.
(1)求y乙(万元)与x(吨)之间的函数关系式.
(2)如果市场准备进甲、乙两种水果共10吨,设乙种水果的进货量为t吨,请你写出这两种水果所获得的销售利润之和W(万元)与t(吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
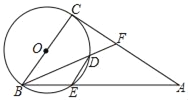
【题目】如图,以BC为直径的⊙O交的边AB于E,点D在⊙O上,且DE∥BC,连BD并延长交CA于F,∠CBF=∠A.
(1)求证:CA是⊙O的切线;
(2)若⊙O的半径为2,BD=2BE,则DE长为 (直接写答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com