
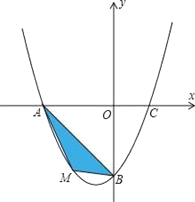
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��x���ཻ��
��x���ཻ��![]() ��C����
��C����![]() ��y���ཻ�ڵ�B
��y���ཻ�ڵ�B![]() ��
��
![]() a0��
a0�� ![]()
![]() �
�![]() ����
����![]() ��
�� ![]() ��
��
![]() ���������߹���ֱ��
���������߹���ֱ��![]() �Գƣ��������ߵĺ�������ʽ��
�Գƣ��������ߵĺ�������ʽ��
![]() ��
��![]() �������£�����MΪ������������������һ���㣬��M�ĺ�����Ϊ
�������£�����MΪ������������������һ���㣬��M�ĺ�����Ϊ![]() �����Ϊ
�����Ϊ![]() ��S����m�ĺ�����ϵʽ�������S�����ֵ��
��S����m�ĺ�����ϵʽ�������S�����ֵ��
![]() ��
��![]() �������£�����P���������ϵĶ��㣬��Q��ֱ��
�������£�����P���������ϵĶ��㣬��Q��ֱ��![]() �ϵĶ��㣬�ж��м���λ���ܹ�ʹ�Ե�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
�ϵĶ��㣬�ж��м���λ���ܹ�ʹ�Ե�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
���𰸡�![]() ��
�� ![]() ����2��
����2��![]() ��
�� ![]() S����m�ĺ�����ϵʽΪ
S����m�ĺ�����ϵʽΪ![]() ��
�� ![]() ʱ��S�����ֵ
ʱ��S�����ֵ![]() ��
�� ![]() ����Ϊ
����Ϊ![]() ��
��![]()
![]() ��
�� ![]()
![]() ��
��![]()
![]() ��
�� ![]()
![]() ��
��![]() ��
��
����������������� ![]() �ɿ������ϣ���֪
�ɿ������ϣ���֪![]() ͼ����
ͼ����![]() �����������㣬��
�����������㣬��![]()
![]() �ɶԳ����֪��
�ɶԳ����֪��![]() ���꣬Ȼ��ѵ�
���꣬Ȼ��ѵ�![]() ��������뺯������ʽ�����ô���ϵ������⼴�ɣ�
��������뺯������ʽ�����ô���ϵ������⼴�ɣ�
![]() ����ͼ�εĸ�����ɵö��κ��������������ߵ�����������������ڶ��κ�������ֵ��Ȼ�ɵý⣻
����ͼ�εĸ�����ɵö��κ��������������ߵ�����������������ڶ��κ�������ֵ��Ȼ�ɵý⣻
![]() �����꣬Ȼ�����
�����꣬Ȼ�����![]() �ij��ȣ��ٸ���ƽ���ı��εĶԱ�����г���ʽ��Ȼ������
�ij��ȣ��ٸ���ƽ���ı��εĶԱ�����г���ʽ��Ȼ������![]() ��һԪ���η��̼��ɵý⣮
��һԪ���η��̼��ɵý⣮
��������� ![]() ��
�� ![]() ��
��
![]() �����߹���ֱ��
�����߹���ֱ��![]() �Գƣ�
�Գƣ� ![]() ��
��
![]()
��![]() ������뺯������ʽ����
������뺯������ʽ����
![]() ��
��
���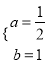 ��
��
���Դ˺�������ʽΪ�� ![]() ��
��
![]() ��ĺ�����Ϊm���ҵ�M�������������ϣ�
��ĺ�����Ϊm���ҵ�M�������������ϣ�
![]() ���������
��������� ![]() ��
��
![]()
![]()
![]()
![]() ��
��
![]() ��
��
��![]() ʱ��S�����ֵΪ��
ʱ��S�����ֵΪ�� ![]() ��
��
��S����m�ĺ�����ϵʽΪ![]() ��
�� ![]() ʱ��S�����ֵ
ʱ��S�����ֵ![]() ��
��
![]() ����Ϊ
����Ϊ![]() ��
��![]()
![]() ��
�� ![]()
![]() ��
��![]()
![]() ��
�� ![]()
![]() ��
��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ��AB��CD��AE��CD�ڵ�C��DE��AE������ΪE����A��30�������D�Ķ�����
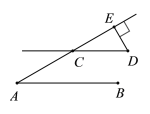
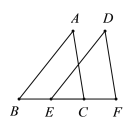
��2����ͼ��E��C��BF�ϣ�AB��DE��AC��DF��BE��CF,��˵����AC��DF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�E,F�ֱ���AB,DC�ϵĵ㣬��
�У�E,F�ֱ���AB,DC�ϵĵ㣬��![]() ������DE,BF,AF.
������DE,BF,AF.
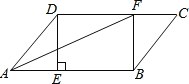
��1����֤���ı���DEBF��ƽ���ı��Σ�
��2����AFƽ��![]() ����AF�ij�.
����AF�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����������ֱ���غ���·l����A��B�����δ���ͷ���۹��C����ͷA�ı�ƫ��60����������ͷB�ı�ƫ��45������AC��4ǧ�ף���ô��ͷA��B֮��ľ������_____ǧ�ף�������������ţ�
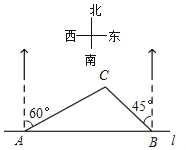
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ֧Ԯ�Ű�������ijѧУ�ƻ��á������������гO�IJ����ʽ����ڹ���A��B�����ͺŵ�ѧϰ��Ʒ��1000������֪A��ѧϰ��Ʒ�ĵ���Ϊ20Ԫ��B��ѧϰ��Ʒ�ĵ���Ϊ30Ԫ��
��1������������ѧϰ��Ʒ����26000Ԫ������A��B����ѧϰ��Ʒ�����ټ���
��2������������ѧϰ��Ʒ��Ǯ������28000Ԫ��������B��ѧϰ��Ʒ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����нⷽ����IJ��ֹ��̣��ش���������
�ⷽ����![]()
������λͬѧ�Ľⷨ���£�
�ⷨһ���ɢ٣���x��2y+5����
�Ѣ۴���ڣ���3(2y+5)��2y��3������
�ⷨ�����٩��ڣ��é�2x��2������
(1)�ⷨһʹ�õľ��巽����________���ⷨ��ʹ�õľ��巽����______���������ַ����Ĺ�ͬ����________��
(2)������ѡһ�ֽⷨ���������Ľ������д����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ����
��ͼ����![]() ��
��![]() ���㣮
���㣮
![]() ��
��![]() ��ȷ������������������һ�κ����ı���ʽ��
��ȷ������������������һ�κ����ı���ʽ��
![]() ��
��![]() ��OB����x����ȡ��C��ʹ
��OB����x����ȡ��C��ʹ![]() ������
������![]() �������
�������
![]() ��
��![]() ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��
ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��
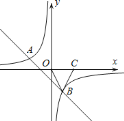
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��MON=90��A�ǡ�MON�ڲ���һ�㣬����A��AB��ON������Ϊ��B��AB=3���ף�OB=4���ף�����E��Fͬʱ��O���������E��1.5����/����ٶ���ON�����˶�����F��2����/����ٶ���OM�����˶���EF��OA���ڵ�C������AE������E�����Bʱ����F��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����t=1��ʱ����EOF�릤ABO�Ƿ����ƣ���˵�����ɡ�
��2�����˶������У�����tȡ��ֵʱ������EF��OA��Ϊʲô��
��3������AF�����˶������У��Ƿ����ijһʱ��t��ʹ��S��AEF=![]() S�ı���ABOF �������ڣ��������ʱt��ֵ���������ڣ���˵�����ɡ�
S�ı���ABOF �������ڣ��������ʱt��ֵ���������ڣ���˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������![]() ����
����![]() �ڷ����У�����ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��Ƚ�
�ڷ����У�����ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��Ƚ�![]() ����ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ��õ�
����ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ��õ�![]() ��
��
![]() �������������ֱ��ǣ�
�������������ֱ��ǣ�![]() ______
______![]() ��
��![]() ______
______![]() ��
��![]() ______
______![]() ��
��
![]() ��ͼ�л���
��ͼ�л���![]() ��
��
![]() ƽ�ƺ�
ƽ�ƺ�![]() ��������������ֱ�Ϊ��
��������������ֱ�Ϊ��![]() ______
______![]() ��
��![]() ______
______![]() ��
��![]() ______
______![]() ��
��
![]() ��y����һ��P��ʹ
��y����һ��P��ʹ![]() ��
��![]() �����ȣ���P�������Ϊ______��
�����ȣ���P�������Ϊ______��
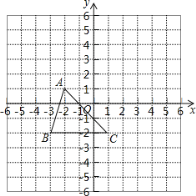
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com