
 如图,在⊙O中,C、D是直径AB上两点,且AC=BD,MC⊥AB,ND⊥AB,M、N在⊙O上.
如图,在⊙O中,C、D是直径AB上两点,且AC=BD,MC⊥AB,ND⊥AB,M、N在⊙O上. |
| AM |
 |
| BN |
 |
| AM |
 |
| MN |
 |
| NB |
 |
| AM |
 |
| BN |
| 1 |
| 2 |
| 1 |
| 2 |
 |
| AM |
 |
| MN |
 |
| NB |
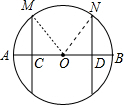 (1)证明:连结OM、ON,如图,
(1)证明:连结OM、ON,如图,
|
 |
| AM |
 |
| BN |
 |
| AM |
 |
| MN |
 |
| NB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 |
| AM |
 |
| MN |
 |
| NB |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
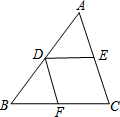 如图所示△ABC中,DE∥BC,DF∥AC,则下列比例式中正确的是( )
如图所示△ABC中,DE∥BC,DF∥AC,则下列比例式中正确的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、(-1,-3) |
| B、(-3,-1) |
| C、(-2,-6) |
| D、(-6,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:
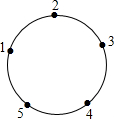 圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移位”后,他到达编号为
圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移位”后,他到达编号为查看答案和解析>>
科目:初中数学 来源: 题型:
| 6 |
| x |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y3<y2<y1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com