
已知关于 的方程
的方程 .
.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角三角形的周长.
(1)证明见解析;
(2)3,4+ 或4+2
或4+2 .
.
【解析】
试题分析:(1)根据关于x的方程x2-(m+2)x+(2m-1)=0的根的判别式的符号来证明结论;
(2)根据一元二次方程的解的定义求得m值,然后由根与系数的关系求得方程的另一根.分类讨论:①当该直角三角形的两直角边是2、3时,由勾股定理得斜边的长度为: ;②当该直角三角形的直角边和斜边分别是2、3时,由勾股定理得该直角三角形的另一直角边为
;②当该直角三角形的直角边和斜边分别是2、3时,由勾股定理得该直角三角形的另一直角边为 ;再根据三角形的周长公式进行计算.
;再根据三角形的周长公式进行计算.
试题解析:(1)证明:∵△=(m+2)2-4(2m-1)=(m-2)2+4,
∴在实数范围内,m无论取何值,(m-2)2+4>0,即△>0,
∴关于x的方程x2-(m+2)x+(2m-1)=0恒有两个不相等的实数根;
(2)【解析】
根据题意,得
12-1×(m+2)+(2m-1)=0,
解得,m=2,
则方程的另一根为:m+2-1=2+1=3;
①当该直角三角形的两直角边是1、3时,由勾股定理得斜边的长度为: ;
;
该直角三角形的周长为1+3+ =4+
=4+ ;
;
②当该直角三角形的直角边和斜边分别是1、3时,由勾股定理得该直角三角形的另一直角边为2 ;则该直角三角形的周长为1+3+2
;则该直角三角形的周长为1+3+2 =4+2
=4+2 .
.
考点:1.根的判别式;2.一元二次方程的解;3.勾股定理.


科目:初中数学 来源:2014-2015学年江苏省无锡市北塘区九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,在Rt△AOB中,OA=OB=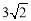 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )

A. B.2 C.
B.2 C. D.
D.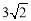
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市八年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题6分)如图,在正方形网格上的一个△ABC.

(1)作△ABC关于直线MN的对称图形(不写作法);
(2)以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出 个三角形与△ABC全等.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市八年级上学期期中考试数学试卷(解析版) 题型:选择题
如果a是b的近似值,那么我们把b叫做a的真值.若用四舍五入法得到的近似值是32,则下列各数不可能是其真值的是( )
A.32.01 B.31.51 C.31.99 D.31.49
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,在⊙O的内接△ABC中,AD⊥BC于D,

(1)①若作直径AP,求证:AB·AC=AD·AP;
②已知AB+AC=12,AD=3,设⊙O的半径为y,AB的长为x.求y与x的函数关系式,及自变量x的取值范围;
(2)图2中,点E为⊙O上一点,且 ,求证:CE+CD=BD.
,求证:CE+CD=BD.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:填空题
在植树节当天,某校一个班同学分成10个小组参加植树造林活动,10个小组植树的株 数见下表:

则这10个小组植树株数的方差是______.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,⊙O的半径为2,点O到直线 的距离为3,点P是直线
的距离为3,点P是直线 上的一个动点,PQ切⊙O于点Q,则PQ的最小值是( )
上的一个动点,PQ切⊙O于点Q,则PQ的最小值是( )

A. B.
B. C.3 D.2
C.3 D.2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市邗江区八年级上学期期中测试数学试卷(解析版) 题型:解答题
(10分)如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.

(1) 在图中画出与关于直线 成轴对称的△A'B'C';
成轴对称的△A'B'C';
(2) 线段CC'被直线 ;
;
(3)△ABC的面积为_______________;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市邗江区九年级上学期期中测试数学试卷(解析版) 题型:选择题
若非零实数 满足
满足 ,则关于x的一元二次方程
,则关于x的一元二次方程 一有一个根为( )
一有一个根为( )
A.3 B.-3 C.0 D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com