
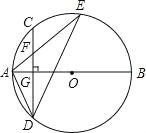
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]()
![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②CD=8;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②CD=8;③tan∠E=![]() ;④S△ADE=6
;④S△ADE=6![]() ,其中正确的有个数是( )
,其中正确的有个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
①利用垂径定理可知弧AC=弧AD,可知∠ADF=∠AED,结合公共角可证明△ADF∽△AED;
②结合CF=2,且![]() =
=![]() ,可求得DF=6,且CG=DG,可求得CD=8;
,可求得DF=6,且CG=DG,可求得CD=8;
③在Rt△AGF中可求得AG,在Rt△AGD中可求得tanADG=![]() ,且∠E=∠ADG,可判断出③;
,且∠E=∠ADG,可判断出③;
④可先求得S△ADF,再求得△ADF∽△AED的相似比和面积比的关系,可求出S△ADE=7![]() .
.
解:①∵AB为直径,AB⊥CD,
∴弧AC=弧AD,
∴∠ADF=∠AED,且∠FAD=∠DAE,
∴△ADF∽△AED,
∴①正确;
②∵AB为直径,AB⊥CD,
∴CG=DG,
∵![]() =
=![]() ,且CF=2,
,且CF=2,
∴FD=6,
∴CD=8,
∴②正确;
③在Rt△AGF中,FG=CG-CF=4-2=2,
∵AF=3,
∴AG=![]() =
=![]() =
=![]() ,且DG=4,
,且DG=4,
∴tan∠ADG=![]() =
=![]() ,
,
∵∠E=∠ADG,
∴tan∠E=![]() ,
,
∴③错误;
④在Rt△ADG中,AG=![]() ,DG=4,
,DG=4,
∴AD=![]() =
=![]() =
=![]() ,
,
由①知:△ADF∽△AED,
∴![]() =(
=(![]() )2,
)2,
∵S△ADF=![]() DFAG=
DFAG=![]() ×6×
×6×![]() =3
=3![]() ,
,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∴S△ADE=7![]() ,
,
∴④错误;
∴正确的有①②,两个.
故选:B.


科目:初中数学 来源: 题型:
【题目】观察下列格式, ![]() -
- ![]() ,
, ![]() ,
, ![]() ,
, ![]() …
…
(1)化简以上各式,并计算出结果;
(2)以上格式的结果存在一定的规律,请按规律写出第5个式子及结果.
(3)用含n(n≥1的整数)的式子写出第n个式子及结果,并给出证明的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,在正方形![]() 中,
中,![]() 是
是![]() 一点,
一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,求证:
,求证:![]() ;
;
拓展:在图①中,若![]() 在
在![]() ,且
,且![]() ,则
,则![]() 成立吗?为什么?
成立吗?为什么?
运用:如图②在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=![]() ,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.
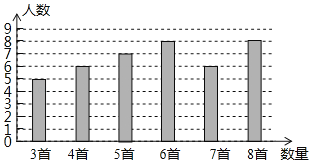
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为_____________,平均数为___________;
(2)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若等腰三角形的一个内角是![]() 则它的另外两个内角的度数是__________,若等腰三角形的一个内角是
则它的另外两个内角的度数是__________,若等腰三角形的一个内角是![]() ,则它的另外两个内角的度数__________.
,则它的另外两个内角的度数__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
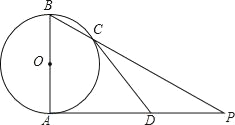
【题目】如图,AB是⊙O的直径,PA是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)若AB=4,∠ABP=60°,求PB的长;
(2)若CD是⊙O的切线.求证:D是AP的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com