
【题目】已知∠ACB=90°,AD平分∠BAC交BC于D,DE⊥AB于E,BE=AE+AF,连结BF,判断△BDF的形状,并说明理由.
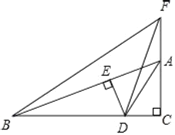
【答案】△BDF是等腰三角形,理由见解析
【解析】
根据角平分线的性质得出DC=DE,再根据全等三角形的判定得出△ACD≌△AED,可得AE=AC,由BE=AE+AF可得出BE=CF,再证明△FCD≌△BED,进而得出BD=FD,则结论得证.
解:△BDF是等腰三角形,理由如下:
∵AD平分∠BAC交BC于D,DE⊥AB于E,∠ACB=90°,
∴DC=DE,
在Rt△ACD和Rt△AED中,
![]() ,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC,
∵BE=AE+AF,
∴BE=AC+AF=CF,
在Rt△FCD和Rt△BED中,
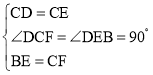 ,
,
∴Rt△FCD≌Rt△BED(SAS),
∴BD=FD,
即△BDF是等腰三角形.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】镇政府想了解李家庄 130 户家庭的经济情况,从中随机抽取了部分家庭进行调查,获得了他们的年收入(单位:万元),并对数据(年收入)进行整理、描述和分析.下面给出了部分信息.
a.被抽取的部分家庭年收入的频数分布直方图和扇形统计图如下(数据分组:0.9≤x<1.3,1.3≤x<1.7 , 1.7≤x<2.1, 2.1≤x<2.5, 2.5≤x<2.9 , 2.9≤x<3.3 )

b.家庭年收入在1.3≤x<1.7 这一组的是: 1.3 1.3 1.4 1.5 1.6 1.6
根据以上信息,完成下列问题:
(1)将两个统计图补充完整;
(2)估计李家庄有多少户家庭年收入不低于 1.5 万元且不足 2.1 万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(提高题) 如图所示,△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.
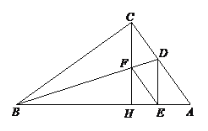
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶店准备从茶农处采购甲、乙两种不同品质的铁观音,已知采购2斤甲型铁观音和1斤乙型铁观音共需要550元,采购3斤甲型铁观音和2斤乙型铁观音共需要900元.
(1)甲、乙两种型号的铁观音每斤分别是多少元?
(2)该茶叶店准备用不超过3500元的资金采购甲、乙两种型号的铁观音共20斤,其中甲种型号的铁观音不少于8斤,采购的斤数需为整数,那么该茶店有几种采购方案?
(3)在⑵的条件下,已知该茶叶店销售甲型铁观音1斤可获利m(m>0)元,销售乙型铁观音1斤可获利50元,则该茶叶店哪种进货方案可获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用列表法画二次函数![]() 的图象时先列一个表,当表中对自变量x的值以相等间隔的值增加时,函数y所对应的值依次为:20、56、110、182、274、380、506、650,其中有一个值不正确,这个不正确的值是( )
的图象时先列一个表,当表中对自变量x的值以相等间隔的值增加时,函数y所对应的值依次为:20、56、110、182、274、380、506、650,其中有一个值不正确,这个不正确的值是( )
A. 506 B. 380 C. 274 D. 182
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式,并探究
①![]()
②![]()
③![]()
……
(1)写出第④个等式:______;
(2)某同学发现,四个连续自然数的积加上1后,结果都将是某一个整数的平方.当这四个数较大时可以进行简便计算,如:
![]() .
.
请你猜想写出第n个等式,用含有n的代数式表示,并通过计算验证你的猜想.
(3)任何实数的平方都是非负数(即![]() ),一个非负数与一个正数的和必定是一个正数(即
),一个非负数与一个正数的和必定是一个正数(即![]() 时,
时,![]() ).根据以上的规律和方法试说明:无论x为什么实数,多项式
).根据以上的规律和方法试说明:无论x为什么实数,多项式![]() 的值永远都是正数.
的值永远都是正数.
查看答案和解析>>
科目:初中数学 来源: 题型:
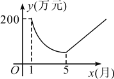
【题目】保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2014年1月的利润为200万元.设2014年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2014年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例,到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
(1)分别求该化工厂治污期间及治污改造工程完工后,y与x之间的函数关系式;
(2)治污改造工程顺利完工后经过几个月,该厂月利润才能达到200万元?
(3)当月利润少于100万元时,为该厂资金紧张期,问该厂资金紧张期共有几个月?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com