
ЁОЬтФПЁПФГВшвЖЕъзМБИДгВшХЉДІВЩЙКМзЁЂввСНжжВЛЭЌЦЗжЪЕФЬњЙлвєЃЌвбжЊВЩЙК2НяМзаЭЬњЙлвєКЭ1НявваЭЬњЙлвєЙВашвЊ550дЊЃЌВЩЙК3НяМзаЭЬњЙлвєКЭ2НявваЭЬњЙлвєЙВашвЊ900дЊЃЎ
ЃЈ1ЃЉМзЁЂввСНжжаЭКХЕФЬњЙлвєУПНяЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉИУВшвЖЕъзМБИгУВЛГЌЙ§3500дЊЕФзЪН№ВЩЙКМзЁЂввСНжжаЭКХЕФЬњЙлвєЙВ20НяЃЌЦфжаМзжжаЭКХЕФЬњЙлвєВЛЩйгк8НяЃЌВЩЙКЕФНяЪ§ашЮЊећЪ§ЃЌФЧУДИУВшЕъгаМИжжВЩЙКЗНАИЃП
ЃЈ3ЃЉдкЂЦЕФЬѕМўЯТЃЌвбжЊИУВшвЖЕъЯњЪлМзаЭЬњЙлвє1НяПЩЛёРћmЃЈm>0ЃЉдЊЃЌЯњЪлвваЭЬњЙлвє1НяПЩЛёРћ50дЊЃЌдђИУВшвЖЕъФФжжНјЛѕЗНАИПЩЛёРћзюЖрЃП
ЁОД№АИЁПЃЈ1ЃЉМзаЭЬњЙлвєУПНя200дЊЃЌвваЭЬњЙлвєУПНя150дЊЃЛЃЈ2ЃЉгаШ§жжЗНАИЃКЂйЙКТђМзаЭКХЬњЙлвє8НяЃЌвваЭКХЬњЙлвє12НяЃЛЂкЙКТђМзаЭКХЬњЙлвє9НяЃЌвваЭКХЬњЙлвє11НяЃЛЂлЙКТђМзаЭКХЬњЙлвє10НяЃЌвваЭКХЬњЙлвє10НяЃЛЃЈ3ЃЉЕБ![]() ЪБЃЌЕквЛжжЗНАИЛёРћзюЖрЃЛЕБ
ЪБЃЌЕквЛжжЗНАИЛёРћзюЖрЃЛЕБ![]() ЪБЃЌШ§жжЗНАИЛёРћвЛбљЃЛ
ЪБЃЌШ§жжЗНАИЛёРћвЛбљЃЛ ![]() ЪБЃЌЕкШ§жжЗНАИЛёРћзюЖрЃЎ
ЪБЃЌЕкШ§жжЗНАИЛёРћзюЖрЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтПЩвдСаГіЯргІЕФЗНГЬзщЃЌДгЖјПЩвдНтД№БОЬтЃЛ
ЃЈ2ЃЉИљОнЬтвтПЩвдЕУЕНЯргІЕФВЛЕШЪНзщЃЌДгЖјПЩвдЧѓЕУгаМИжжВЩЙКЗНАИЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉжаЕФЙКТђЗНАИМЦЫуГіШ§жжЗНАИЕФРћШѓЃЌШЛКѓдйНјааБШНЯМДПЩЃЎ
НтЃКЃЈ1ЃЉЩшМзаЭЬњЙлвєЕЅМл![]() дЊ/НяЃЌвваЭЬњЙлвєЬњЙлвєЕЅМл
дЊ/НяЃЌвваЭЬњЙлвєЬњЙлвєЕЅМл![]() дЊ/НяЃЌ
дЊ/НяЃЌ
СаЗНГЬзщЕУЃК![]()
НтЕУЃК![]()
ОМьбщЗћКЯЬтвтЃЌ
Д№ЃКМзаЭЬњЙлвєУПНя200дЊЃЌвваЭЬњЙлвєУПНя150дЊЃЎ
ЃЈ2ЃЉЩшЙКТђМзаЭКХЬњЙлвє![]() НяЃЌдђЙКТђвваЭКХЬњЙлвє
НяЃЌдђЙКТђвваЭКХЬњЙлвє![]() НяЃЌвРЬтвтЕУЃЌ
НяЃЌвРЬтвтЕУЃЌ
![]()
НтЕУ![]() ЃЌ
ЃЌ
гжЁп![]() ЮЊећЪ§
ЮЊећЪ§
Ёр![]()
ЫљвдгаШ§жжЗНАИШчЯТЃК
ЂйЙКТђМзаЭКХЬњЙлвє8НяЃЌвваЭКХЬњЙлвє12НяЃЛ
ЂкЙКТђМзаЭКХЬњЙлвє9НяЃЌвваЭКХЬњЙлвє11НяЃЛ
ЂлЙКТђМзаЭКХЬњЙлвє10НяЃЌвваЭКХЬњЙлвє10НяЃЛ
ЃЈ3ЃЉгаЃЈ2ЃЉЕУЃЌШ§жжЗНАИПЩЛёРћЧщПіЃК
ЗНАИвЛЃК![]() ЃЈдЊЃЉ
ЃЈдЊЃЉ
ЗНАИЖўЃК![]() ЃЈдЊЃЉ
ЃЈдЊЃЉ
ЗНАИШ§ЃК![]() ЃЈдЊЃЉ
ЃЈдЊЃЉ
ЁрЕБ![]() ЪБЃЌЕквЛжжЗНАИЛёРћзюЖрЃЛ
ЪБЃЌЕквЛжжЗНАИЛёРћзюЖрЃЛ
ЕБ![]() ЪБЃЌШ§жжЗНАИЛёРћвЛбљЃЛ
ЪБЃЌШ§жжЗНАИЛёРћвЛбљЃЛ
![]() ЪБЃЌЕкШ§жжЗНАИЛёРћзюЖрЃЎ
ЪБЃЌЕкШ§жжЗНАИЛёРћзюЖрЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() гкЕу
гкЕу![]()
ЃЈ1ЃЉШчЭМ1ЃЌШє![]() ЕФНЧЦНЗжЯпНЛ
ЕФНЧЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() ЗжБ№дкЯпЖЮ
ЗжБ№дкЯпЖЮ![]() ЩЯЃЌНЋ
ЩЯЃЌНЋ![]() елЕўЃЌЕу
елЕўЃЌЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌЕу
ДІЃЌЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌелКлЗжБ№ЮЊ
ДІЃЌелКлЗжБ№ЮЊ![]() КЭ
КЭ![]() ЃЌЧвЕу
ЃЌЧвЕу![]() ЃЌЕу
ЃЌЕу![]() ОљдкжБЯп
ОљдкжБЯп![]() ЩЯЃЌШє
ЩЯЃЌШє![]() ЃЌЪдВТЯы
ЃЌЪдВТЯы![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЛ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉаЁЬтЕФЬѕМўЯТЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊвЛИіНЧЖШ
ФцЪБеыа§зЊвЛИіНЧЖШ![]() ЃЈ
ЃЈ![]() ЃЉЃЌМЧа§зЊжаЕФ
ЃЉЃЌМЧа§зЊжаЕФ![]() ЮЊ
ЮЊ![]() ЃЈШчЭМ3ЃЉЃЌдка§зЊЙ§ГЬжаЃЌжБЯп
ЃЈШчЭМ3ЃЉЃЌдка§зЊЙ§ГЬжаЃЌжБЯп![]() гыжБЯп
гыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() гыжБЯп
гыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌЪЧЗёДцдкетбљЕФ
ЃЌЪЧЗёДцдкетбљЕФ![]() СНЕуЃЌЪЙ
СНЕуЃЌЪЙ![]() ЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіа§зЊНЧ
ЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіа§зЊНЧ![]() ЕФЖШЪ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФЖШЪ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЁїABCжаЃЌABЃНACЃЌBDЃЌCEЪЧНЧЦНЗжЯпЃЌЭМжаЕФЕШбќШ§НЧаЮЙВга( )

A. 6Иі B. 5Иі C. 4Иі D. 3Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФБпаЮABCDЮЊОиаЮЃЌAD=20cmЁЂAB=10cmЃЎMЕуДгDЕНAЃЌPЕуДгBЕНCЃЌСНЕуЕФЫйЖШЖМЮЊ2cm/sЃЛNЕуДгAЕНBЃЌQЕуДгCЕНDЃЌСНЕуЕФЫйЖШЖМЮЊ1cm/sЃЎШєЫФИіЕуЭЌЪБГіЗЂЃЎ
ЃЈ1ЃЉХаЖЯЫФБпаЮMNPQЕФаЮзДЃЎ
ЃЈ2ЃЉЫФБпаЮMNPQФмЮЊСтаЮТ№ЃПШєФмЃЌЧыЧѓГіДЫЪБдЫЖЏЕФЪБМфЃЛШєВЛФмЃЌЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
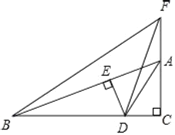
ЁОЬтФПЁПвбжЊЁЯACBЃН90ЁуЃЌADЦНЗжЁЯBACНЛBCгкDЃЌDEЁЭABгкEЃЌBEЃНAE+AFЃЌСЌНсBFЃЌХаЖЯЁїBDFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОХФъМЖЃЈ1ЃЉАрПЮЭтЛюЖЏаЁзщРћгУБъИЫВтСПбЇаЃЦьИЫЕФИпЖШЃЌШчЭМЫљЪОЃЌвбжЊБъИЫИпЖШCD=3mЃЌБъИЫгыЦьИЫЕФЫЎЦНОрРыBD=15mЃЌШЫЕФблОІгыЕиУцЕФИпЖШEF=1.6mЃЌШЫгыБъИЫCDЕФЫЎЦНОрРыDF=2mЃЌдђЦьИЫABЕФИпЖШ mЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌЦфжаAЕузјБъЮЊ
ЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌЦфжаAЕузјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЃЌСэХзЮяЯпОЙ§Еу
ЃЌСэХзЮяЯпОЙ§Еу![]() ЃЌMЮЊЫќЕФЖЅЕуЃЎ
ЃЌMЮЊЫќЕФЖЅЕуЃЎ
![]() ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
![]() Чѓ
Чѓ![]() ЕФУцЛ§
ЕФУцЛ§![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌAЃЈ2ЃЌ2ЃЉЃЎ
ЃЈЂёЃЉШєЕуBЃЈ4ЃЌ2ЃЉЃЌCЃЈ3ЃЌ5ЃЉЃЌЧыХаЖЯЁїABCЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈЂђЃЉвбжЊЕуMЃЈmЃЌ0ЃЉЃЌNЃЈ0ЃЌnЃЉЃЈnЃМ0ЃЉЃЌШєЁЯMANЃН90ЁуЃЌЧвmnЃНЉ![]() ЃЌЧѓm2+n2ЕФжЕЃЎ
ЃЌЧѓm2+n2ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСНЬѕЛЅЯрЦНааЕФКгАЖЃЌдкКгАЖвЛБпВтЕУABЮЊ20УзЃЌдкСэвЛБпВтЕУCDЮЊ70УзЃЌгУВтНЧЦїВтЕУЁЯACD=30ЁуЃЌВтЕУЁЯBDC=45ЁуЃЌЧѓСНЬѕКгАЖжЎМфЕФОрРыЃЎЃЈ![]() ЃЌ
ЃЌ ![]() Ёж1.7ЃЌНсЙћБЃСєећЪ§ЃЉ
Ёж1.7ЃЌНсЙћБЃСєећЪ§ЃЉ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com