
【题目】已知:如图,二次函数![]() 的图象与x轴交于A、B两点,其中A点坐标为
的图象与x轴交于A、B两点,其中A点坐标为![]() ,点
,点![]() ,另抛物线经过点
,另抛物线经过点![]() ,M为它的顶点.
,M为它的顶点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 求
求![]() 的面积
的面积![]() .
.

【答案】
【1】
【2】
【解析】
(1)由A、C、D三点在抛物线上,根据待定系数法即可求出抛物线的解析式;
(2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=![]() MNOB.
MNOB.
(1)∵A(-1,0),C(0,5),D(1,8)三点在抛物线y=ax2+bx+c上,
∴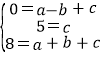 ,
,
解方程组,得 ,
,
故抛物线的解析式为y=-x2+4x+5;
(2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=![]() MNOB.
MNOB.
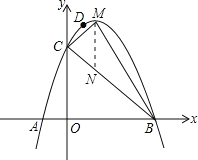
∵y=-x2+4x+5=-(x-5)(x+1)=-(x-2)2+9,
∴M(2,9),B(5,0),
由B、C两点的坐标易求得直线BC的解析式为:y=-x+5,
当x=2时,y=-2+5=3,则N(2,3),
则MN=9-3=6,
则S△MCB=![]() ×6×5=15.
×6×5=15.
本题考查了解二次函数综合题的方法:先运用待定系数法求出二次函数的解析式,确定各特殊点的坐标,得到有关线段的长,求出三角形的面积.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A. 中位数是6.5 B. 平均数高于众数
C. 极差为3 D. 平均每周锻炼超过6小时的人占总数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶店准备从茶农处采购甲、乙两种不同品质的铁观音,已知采购2斤甲型铁观音和1斤乙型铁观音共需要550元,采购3斤甲型铁观音和2斤乙型铁观音共需要900元.
(1)甲、乙两种型号的铁观音每斤分别是多少元?
(2)该茶叶店准备用不超过3500元的资金采购甲、乙两种型号的铁观音共20斤,其中甲种型号的铁观音不少于8斤,采购的斤数需为整数,那么该茶店有几种采购方案?
(3)在⑵的条件下,已知该茶叶店销售甲型铁观音1斤可获利m(m>0)元,销售乙型铁观音1斤可获利50元,则该茶叶店哪种进货方案可获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用列表法画二次函数![]() 的图象时先列一个表,当表中对自变量x的值以相等间隔的值增加时,函数y所对应的值依次为:20、56、110、182、274、380、506、650,其中有一个值不正确,这个不正确的值是( )
的图象时先列一个表,当表中对自变量x的值以相等间隔的值增加时,函数y所对应的值依次为:20、56、110、182、274、380、506、650,其中有一个值不正确,这个不正确的值是( )
A. 506 B. 380 C. 274 D. 182
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元进行批量生产,已知生产每件产品的成本为40元.在销售过程中发现,年销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利(年获利=年销售额-生产成本-投资)为z(万元).
(1)试写出y与x之间的函数关系式(不必写出x的取值范围);
(2)试写出z与x之间的函数关系式(不必写出x的取值范围);
(3)计算销售单价为160元时的年获利,并说明同样的年获利,销售单价还可定为多少元?相应的年销售量分别为多少万件?
(4)公司计划:在第一年按年获利最大确定的销售单价,进行销售;第二年年获利不低于1130万元.请你借助函数的大致图象说明,第二年的销售单价x(元)应确定在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式,并探究
①![]()
②![]()
③![]()
……
(1)写出第④个等式:______;
(2)某同学发现,四个连续自然数的积加上1后,结果都将是某一个整数的平方.当这四个数较大时可以进行简便计算,如:
![]() .
.
请你猜想写出第n个等式,用含有n的代数式表示,并通过计算验证你的猜想.
(3)任何实数的平方都是非负数(即![]() ),一个非负数与一个正数的和必定是一个正数(即
),一个非负数与一个正数的和必定是一个正数(即![]() 时,
时,![]() ).根据以上的规律和方法试说明:无论x为什么实数,多项式
).根据以上的规律和方法试说明:无论x为什么实数,多项式![]() 的值永远都是正数.
的值永远都是正数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售的篮球和足球的进货价格分别是每个30元,40元.商场销售5个篮球和1个足球,可获利76元;销售6个篮球和3个足球,可获利120元.
(1)求该商场篮球和足球的销售价格分别是多少?
(2)商场准备用不多于2500元的资金购进篮球和足球共70个,问最少需要购进篮球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
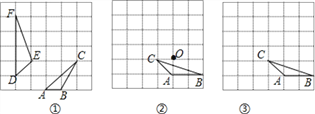
【题目】如图,在![]() 的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形,
的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形, ![]() 是一个格点三角形.
是一个格点三角形.
![]() 在图
在图![]() 中,请判断
中,请判断![]() 与
与![]() 是否相似,并说明理由;
是否相似,并说明理由;
![]() 在图
在图![]() 中,以O为位似中心,再画一个格点三角形,使它与
中,以O为位似中心,再画一个格点三角形,使它与![]() 的位似比为2:1
的位似比为2:1
![]() 在图
在图![]() 中,请画出所有满足条件的格点三角形,它与
中,请画出所有满足条件的格点三角形,它与![]() 相似,且有一条公共边和一个公共角.
相似,且有一条公共边和一个公共角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com