
����Ŀ����ͼ����֪������y=��x2+2x+3��x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C������BC��

��1����A��B��C��������ꣻ
��2������PΪ�߶�BC��һ�㣨����B��C�غϣ���PM��y�ᣬ��PM���������ڵ�M����x���ڵ�N������BCM��������ʱ�����P�����ꣻ
��3���ڣ�2���������£�����BCM��������ʱ���������ߵĶԳ����ϴ���һ��Q��ʹ����CNQΪֱ�������Σ����Q�����꣮
���𰸡���1��C��0��3����A����1��0����B��3��0������2����t=![]() ʱ����BCM��������ʱP������Ϊ��
ʱ����BCM��������ʱP������Ϊ��![]() ��
�� ![]() ������3��Q���������1��
������3��Q���������1�� ![]() ����1��
����1�� ![]() ����1��
����1�� ![]() ����1����
����1����![]() ��.
��.
�������������������1���������߽���ʽ�У���x=0�����C�����꣬��y=0������A��B�����ꣻ��2����B��C����������ֱ��BC�Ľ���ʽΪy=��x+3������P������Ϊ��t����t+3������ɱ�ʾ��M�����꣬������PM�ij����Ӷ�����t��ʾ����BCM������������ö��κ��������ʿ���õ���BCM��������ʱt��ֵ�������P�����ꣻ
��3���ɣ�2����֪N�����꣬��Q������Ϊ��1��m���������m�ֱ��ʾ��QN��QC��CN���ֵ�CΪֱ�Ƕ��㡢��QΪֱ�Ƕ���͵�NΪֱ�Ƕ�������������ֱ���ݹ��ɶ����ɵõ�����m�ķ��̣������m��ֵ�������Q�����꣮
����������⣺��1����y=��x2+2x+3�У���x=0�ɵ�y=3������C��0��3������y=0���ɵé�x2+2x+3=0�����x=3��x=��1����A����1��0����B��3��0����
��2����ֱ��BC�Ľ���ʽΪy=kx+b�����У� ![]() ����ã�
����ã� ![]() ����ֱ��BC�Ľ���ʽΪy=��x+3����P��t����t+3������M��t����t2+2t+3������PM=����t2+2t+3��������t+3��=��t2+3t����S��BCM=
����ֱ��BC�Ľ���ʽΪy=��x+3����P��t����t+3������M��t����t2+2t+3������PM=����t2+2t+3��������t+3��=��t2+3t����S��BCM=![]() PM��ON+BN��=
PM��ON+BN��= ![]() PMOB=
PMOB= ![]() ��3����t2+3t��=��
��3����t2+3t��=��![]() ��t��
��t�� ![]() ��2+
��2+ ![]() ���ߩ�
���ߩ� ![]() ��0���൱t=
��0���൱t= ![]() ʱ����BCM��������ʱP������Ϊ��
ʱ����BCM��������ʱP������Ϊ�� ![]() ��
�� ![]() ��
��
��3����y=��x2+2x+3=����x��1��2+4���������ߵĶԳ���Ϊֱ��x=1������Q��1��m������C��0��3����N��![]() ��0������CN=
��0������CN=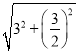 =
=![]() ��CQ=
��CQ= ![]() =
=![]() ��NQ=
��NQ=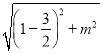 =
= ![]() ���ߡ�CNQΪֱ�������Σ���ֵ�CΪֱ�Ƕ��㡢��QΪֱ�Ƕ���͵�NΪֱ�Ƕ������������
���ߡ�CNQΪֱ�������Σ���ֵ�CΪֱ�Ƕ��㡢��QΪֱ�Ƕ���͵�NΪֱ�Ƕ������������
�ٵ���CΪֱ�Ƕ���ʱ������CN2+CQ2=NQ2 ������![]() ��2+��m2��6m+10��=
��2+��m2��6m+10��= ![]() +m2 �����m=
+m2 �����m=![]() ����ʱQ������Ϊ��1��
����ʱQ������Ϊ��1�� ![]() ����
����
�ڵ���QΪֱ�Ƕ���ʱ������NQ2+CQ2=CN2 ������m2��6m+10��+ ![]() +m2=��
+m2=�� ![]() ��2 �����x=
��2 �����x= ![]() ��x=
��x= ![]() ����ʱQ������Ϊ��1��
����ʱQ������Ϊ��1�� ![]() ����1��
����1�� ![]() ����
����
�۵���NΪֱ�Ƕ���ʱ������NQ2+CN2=CQ2 ������ ![]() ��2+
��2+ ![]() +m2=m2��6m+10�����m=��
+m2=m2��6m+10�����m=�� ![]() ����ʱQ������Ϊ��1����
����ʱQ������Ϊ��1����![]() ����
����
���Ͽ�֪Q�������Ϊ��1�� ![]() ����1��
����1�� ![]() ����1��
����1�� ![]() ����1����
����1����![]() ����
����


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д� ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������֯һ���ο�������Σ�ԭ�ƻ�����30���ͳ�������������15��û����λ��������ͬ��������45���ͳ�������һ������������ͳ�ǡ����������֪30���ͳ����Ϊÿ��220Ԫ��45���ͳ����Ϊÿ��300Ԫ���ʣ�
��1�������ο͵��������Ƕ��٣�ԭ�ƻ����ö�����30���ͳ���
��2��������ͬһ�ֿͳ���Ҫʹÿλ�οͶ�����λ��Ӧ���������òź��㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǵȱߡ�ABC��һ�㣬D�ǡ�ABC���һ�㣬��AOB=110������BOC=������BOC�ա�ADC����OCD=60��������OD��
��1����֤����OCD�ǵȱ������Σ�
��2������=150��ʱ�����жϡ�AOD����״�����Ƿ��ࣩ����˵�����ɣ�
��3�����OAD�Ķ�����
��4��̽��������=�� ��ʱ����AOD�ǵ��������Σ�������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�٣�ֱ��MN��ֱ��PQ������ΪO����A������OP�ϣ���B������OQ�ϣ�A��B����O���غϣ�����C������ON�ϣ�����C��ֱ��![]() ����D�ڵ�C����ߡ�
����D�ڵ�C����ߡ�
��1����BDƽ�֡�ABC��![]() ����
����![]() _____����
_____����
��2����ͼ�ڣ���![]() ������CBA��ƽ���߽�OC��E����AC��F����˵��
������CBA��ƽ���߽�OC��E����AC��F����˵��![]() ��
��
��3����ͼ�ۣ�����ADC=��DAC����B������OQ���˶�����ACB��ƽ���߽�DA���ӳ����ڵ�H.�ڵ�B�˶�������![]() ��ֵ�Ƿ�仯�������䣬�����ֵ�����仯������仯��Χ.
��ֵ�Ƿ�仯�������䣬�����ֵ�����仯������仯��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ij��һ���ƺ�ϵ��Զ���ת��ˮװ�ã�������ת��ˮװ�õ���ת�Ƕ�Ϊ240���������������һ�����Σ�С��ͬѧ���˽�����װ���ܹ����IJ�ƺ���������������������ݣ���������ʾ��ͼ����ͼ2��A��B����ľ���Ϊ18�ף�������װ���ܹ����IJ�ƺ�����
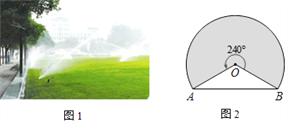
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
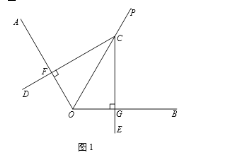
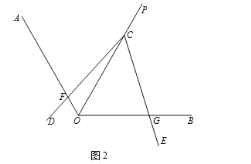
����Ŀ����֪OPƽ�֡�AOB����DCE�Ķ���C������OP�ϣ�����CD������OA�ڵ�F������CE������OB�ڵ�G��
��1����ͼ1����CD��OA��CE��OB����ֱ��д���߶�CF��CG��������ϵ��
��2����ͼ2������AOB=120����DCE=��AOC�����ж��߶�CF��CG��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ�麣�������н��裬����ij��ˮ������˾���ϸĽ���ˮ�����豸�����豸ÿСʱ������ˮ����ԭϵͳ��1.5����ԭ������1200m3��ˮ���õ�ʱ������ڶ���10Сʱ��
��1��ԭ��ÿСʱ������ˮ���Ƕ���m2��
��2���������豸������ˮ960m3����Ҫ�ʱ�䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��ͼ��������ABC�У�D��BC����һ��.
(1)����D��AB��AC��ƽ���߷ֱ�AB�ڵ�E,��AC�ڵ�F;
(2)˵��:��EDF=��A;
(3)˵��:��A+��B+��C=180��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��5��26��������ĵ���������������ʡ������¡���ٿ���ijУ��֯����ʦ��ǰ���ι�ѧϰ,����A��B�����ͺŵ����γ���8����һ��A�ͳ�����40��,һ��B�ͳ�����35�ˡ�
(1)��ǰ���ι۵�ʦ����310��,Ϊ�˸պý�ȫ��ʦ���ʹ�Ŀ�ĵ�,Ӧ�ֱ�����A��B�����ͺŵ����γ���������?
(2)��A�ͺŵij�ÿ�������220Ԫ,B�ͺŵij�ÿ�������160Ԫ,ѧУҪ��������ò�����1540Ԫ,��ô�������ö�����A�ͺŵ����γ�?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com