
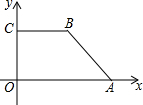
 如图所示的平面直角坐标系中,在直角梯形OABC中,CB∥OA,CB=8,OC=6,∠OAB=45°.
如图所示的平面直角坐标系中,在直角梯形OABC中,CB∥OA,CB=8,OC=6,∠OAB=45°. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
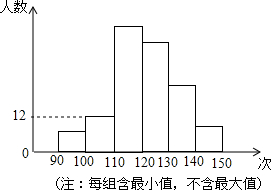 九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,测试成绩整理后作出如图统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率和为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题
九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,测试成绩整理后作出如图统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率和为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4 | B. | $-\frac{1}{4}$ | C. | 4 | D. | $-\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com