
【题目】在平面直角坐标系中,△AOB为等边三角形,B(2,0),直线l:y=kx+b经过点B,点C是x轴正半轴上的一动点,以线段AC为边在第一象限作等边△ACD.
(1)直接写出点A的坐标:A( , ),当直线l经过点A时,求直线BA的表达式.
(2)当直线l经过点D时,直线与y轴相交于点F,随着点C的变化,点F的位置是否发生变化?若没有变化,求出此时点F的坐标.;若有变化,请说明理由.
(3)当直线与线段OA相交与点E时,如果直线l把△AOB的面积分为1:2两部分,求出此时点E的坐标.
(4)若点C的坐标为(4,0)时,直线l与线段AD有交点,请直接写出此时k的取值范围.
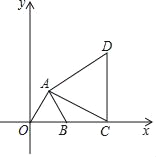
【答案】(1)A(1,![]() );(2)点F的位置不会发生变化,为F(0,-2
);(2)点F的位置不会发生变化,为F(0,-2![]() );(3) E(
);(3) E(![]() ,
,![]() ),E′(
),E′(![]() ,
,![]() );(4)x≤
);(4)x≤![]() 或者x≥
或者x≥![]()
【解析】
(1)如图,作AH⊥OB于H,解直角三角形求出AH即可,利用待定系数法求出直线AB的解析式即可;
(2)由△OAC≌△BAD(SAS),推出BD∥OA,求出直线BD的解析式即可解决问题;
(3)分两种情况分别求解即可解决问题;
(4)求出直线AB,BD的解析式即可判断k的取值范围.
解:(1)如图,作AH⊥OB于H.
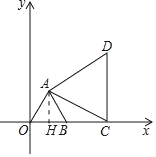
∵B(2,0),△ABC是等边三角形,
∴OA=OB=AB=2,
∵AH⊥OB,
∴OH=HB=1,
∴AH=![]() =
=![]()
∴A(1,![]() ),
),
把A,B坐标代入y=kx+b得到:![]() ,
,
解之得![]() ,
,
所以直线AB解析式为![]() .
.
故答案为1,![]() .
.
(2)作直线BD,由已知AO=AB,AC=AO,

又∠OAB=∠CAD,
∠OAB+∠BAC=∠CAD+∠BAC
∠OAC=∠BAD
△OAC≌△BAD(SAS)
∠AOC=∠ABD=60°,
∵∠OAB=∠AOB=60°,
∴∠OAB=∠ABD=60°,
∴BD∥OA
∵直线OA的解析式为![]() ,
,
设直线BD:![]() ,则
,则![]() ,
,
所以b1=![]() ,
,
即点F的位置不会发生变化,为F(0,![]() ).
).
(3)有两种情况,
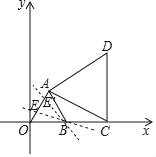
当OE=![]() OA或OE′=
OA或OE′=![]() OA时,满足条件,
OA时,满足条件,
∵A(1,![]() ),
),
∴E(![]() ,
,![]() ),E′(
),E′(![]() ,
,![]() );
);
(4)如图,
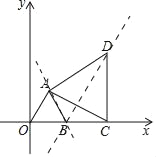
当C(4,0)时,易知:AB=BC=2,
∴∠BAC=∠BCA,
∵∠ABO=60°=∠BAC+∠BCA,
∴∠BCA=∠BAC=30°,
∵∠ACD=∠OAB=60°,
∴∠DCB=∠OAC=90°,
∴AC=![]() OA=2
OA=2![]() ,
,
∴D(4,2![]() ),
),
∵直线AB的解析式为y=﹣![]() +2
+2![]() ,
,
当直线l经过点D时,直线l的解析式为y=![]() x﹣2
x﹣2![]() ,
,
观察图象可知满足条件的k的值为x≤![]() 或者x≥
或者x≥![]() .
.


科目:初中数学 来源: 题型:
【题目】在同一直角坐标系中,直线y=﹣x+3与y=3x﹣5相交于C点,分别与x轴交于A、B两点.P、Q分别为直线y=﹣x+3与y=3x﹣5上的点.
(1)求△ABC的面积;
(2)若P、Q关于原点成中心对称,求P点的坐标;
(3)若△QPC≌△ABC,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题: 
(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1). ①画出△ABC关于y轴对称的△A1B1C1 , 并写出点C1的坐标;
②连结BC1 , 在坐标平面的格点上确定一个点P,使△B C1P是以B C1为底的等腰直角三角形,画出△B C1P,并写出所有P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如下:
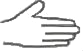 ﹣3x=x2﹣5x+1
﹣3x=x2﹣5x+1
(1)求所捂的二次三项式;
(2)若x=![]() +1,求所捂二次三项式的值;
+1,求所捂二次三项式的值;
(3)如果![]() +1的整数部分为a,则a2= .
+1的整数部分为a,则a2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一部记录片播放了关于地震的资料及一个有关地震预测的讨论,一位专家指出:“在未来20年,A城市发生地震的机会是三分之二”
对这位专家的陈述下面有四个推断:
①![]() ×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
②![]() 大于50%,所以未来20年,A城市一定发生地震;
大于50%,所以未来20年,A城市一定发生地震;
③在未来20年,A城市发生地震的可能性大于不发生地震的可能性;
④不能确定在未来20年,A城市是否会发生地震;
其中合理的是( )
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
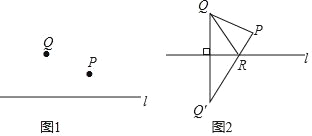
如图1,P,Q是直线l同侧两点,请你在直线l上确定一个点R,使△PQR的周长最小.
小阳的解决方法如下:
如图2,
(1)作点Q关于直线l的对称点Q;
(2)连接PQ′交直线l于点R;
(3)连接RQ,PQ.
所以点R就是使△PQR周长最小的点.
老师说:“小阳的作法正确.”
请回答:小阳的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P与正方形的边碰撞的次数为 , 小球P所经过的路程为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com