
【题目】已知直角梯形ABCD中,AD∥BC,∠A=90°,△BCD为等边三角形,且AD=![]() ,则梯形的周长是_______.
,则梯形的周长是_______.
【答案】![]() +5
+5![]() ;
;
【解析】
先根据△BCD是等边三角形,可得∠2=60°,BC=CD=BD,而AD∥BC,∠A=90°,根据平行线的性质可求∠ABC=90°,进而可求∠1=30°,利用直角三角形中30°的角所对的直角边等于斜边的一半,易求BD,再根据勾股定理可求AB,从而可求梯形的周长.
如图,
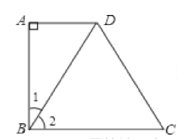
∵△BCD是等边三角形,
∴∠2=60°,BC=CD=BD,
∵AD∥BC,∠A=90°,
∴∠ABC+∠A=180°,
∴∠ABC=90°,
∴∠1=90°60°=30°,
在Rt△ABD中,∵∠1=30°,AD=![]() ,
,
∴BD=2AD=2![]() ,AB=
,AB=![]() ,
,
∴梯形ABCD的周长=AD+AB+BC+CD=![]() +
+![]() +2
+2![]() +2
+2![]() =
=![]() +5
+5![]() .
.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:若![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 的距离的2倍,我们就称点
的距离的2倍,我们就称点![]() 是
是![]() 的优点. 例如图1中:点
的优点. 例如图1中:点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为2. 表示1的点
表示的数为2. 表示1的点![]() 到点
到点![]() 的距离是2,到点
的距离是2,到点![]() 的距离是1,那么点
的距离是1,那么点![]() 是
是![]() 的优点;又如,表示0的点
的优点;又如,表示0的点![]() 到点
到点![]() 的距离是1,到点
的距离是1,到点![]() 的距离是2,那么点
的距离是2,那么点![]() 就不是
就不是![]() 的优点,但点
的优点,但点![]() 是
是![]() ,的优点.
,的优点.
知识运用:(1)如图2,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为4. 那么数________所表示的点是
所表示的数为4. 那么数________所表示的点是![]() 的优点;(直接填在横线上)
的优点;(直接填在横线上)
(2)如图3,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为40. 现有一只电子蚂蚁
所表示的数为40. 现有一只电子蚂蚁![]() 从点
从点![]() 出发,以4个单位每秒的速度向左运动,到达点
出发,以4个单位每秒的速度向左运动,到达点![]() 停止. 当
停止. 当![]() 为何值时,
为何值时,![]() 、
、![]() 和
和![]() 中恰有一个点为其余两点的优点?
中恰有一个点为其余两点的优点?
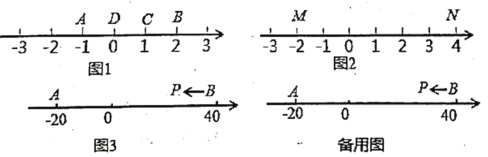
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当前,“精准扶贫”工作已进入攻坚阶段,凡贫困家庭均要“建档立卡”![]() 某初级中学七年级共有四个班,已“建档立卡”的贫困家庭的学生人数按一、二、三、四班分别记为
某初级中学七年级共有四个班,已“建档立卡”的贫困家庭的学生人数按一、二、三、四班分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,现对
,现对![]() ,
,![]() ,
,![]() ,
,![]() 统计后,制成如图所示的统计图.
统计后,制成如图所示的统计图.
![]() 求七年级已“建档立卡”的贫困家庭的学生总人数;
求七年级已“建档立卡”的贫困家庭的学生总人数;
![]() 将条形统计图补充完整,并求出
将条形统计图补充完整,并求出![]() 所在扇形的圆心角的度数;
所在扇形的圆心角的度数;
![]() 现从
现从![]() ,
,![]() 中各选出一人进行座谈,若
中各选出一人进行座谈,若![]() 中有一名女生,
中有一名女生,![]() 中有两名女生,请用树状图表示所有可能情况,并求出恰好选出一名男生和一名女生的概率.
中有两名女生,请用树状图表示所有可能情况,并求出恰好选出一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上.
上.
(1)若点![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)连接![]() ,若点
,若点![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,且交直线
,且交直线![]() 于点
于点![]() .若
.若![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
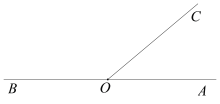
【题目】如图,已知点O在直线AB上,作射线OC,点D在平面内,∠BOD与∠AOC互余.
(1)若∠AOC:∠BOD=4:5,则∠BOD= ;
(2)若∠AOC=α(0°<α≤45°),ON平分∠COD.
①当点D在∠BOC内,补全图形,直接写出∠AON的值(用含α的式子表示);
②若∠AON与∠COD互补,求出α的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,点M、N分别是AD、BC的中点,如果BC=10,AD=4,那么MN的长是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边
的边![]() 在数轴上,数轴上点
在数轴上,数轴上点![]() 表示的数为
表示的数为![]() ,正方形
,正方形![]() 的面积为16.
的面积为16.
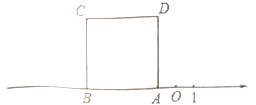
(1)数轴上点![]() 表示的数为__________;
表示的数为__________;
(2)将正方形![]() 沿数轴水平移动,移动后的正方形记为
沿数轴水平移动,移动后的正方形记为![]() ,移动后的正方形
,移动后的正方形![]() 与原正方形
与原正方形![]() 重叠部分的面积记为
重叠部分的面积记为![]() .当
.当![]() 时,画出图形,并求出数轴上点
时,画出图形,并求出数轴上点![]() 表示的数;
表示的数;
查看答案和解析>>
科目:初中数学 来源: 题型:
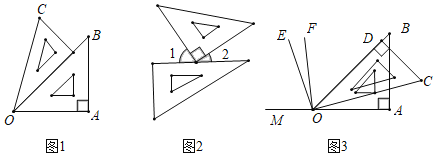
【题目】借助一副三角板,可以得到一些平面图形
(1)如图1,∠AOC= 度.由射线OA,OB,OC组成的所有小于平角的和是多少度?
(2)如图2,∠1的度数比∠2度数的3倍还多30°,求∠2的度数;
(3)利用图3,反向延长射线OA到M,OE平分∠BOM,OF平分∠COM,请按题意补全图(3),并求出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用如图1所示的曲尺形框框(有三个方向),可以套住图2日历中的三个数,设被框住的三个数中(第一个框框住的最大的数为![]() 、第二个框框住的最大的数为
、第二个框框住的最大的数为![]() 、第三个框框住的最大的数为
、第三个框框住的最大的数为![]() )
)

(1)第一个框框住的三个数的和是: ,第二个框框住的三个数的和是: ,第三个框框住的三个数中的和是: ;
(2)这三个框框住的数的和分别能是81吗?若能,则分别求出最大的数![]() 、
、![]() 、
、![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com