
【题目】阅读理解:若![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 的距离的2倍,我们就称点
的距离的2倍,我们就称点![]() 是
是![]() 的优点. 例如图1中:点
的优点. 例如图1中:点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为2. 表示1的点
表示的数为2. 表示1的点![]() 到点
到点![]() 的距离是2,到点
的距离是2,到点![]() 的距离是1,那么点
的距离是1,那么点![]() 是
是![]() 的优点;又如,表示0的点
的优点;又如,表示0的点![]() 到点
到点![]() 的距离是1,到点
的距离是1,到点![]() 的距离是2,那么点
的距离是2,那么点![]() 就不是
就不是![]() 的优点,但点
的优点,但点![]() 是
是![]() ,的优点.
,的优点.
知识运用:(1)如图2,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为4. 那么数________所表示的点是
所表示的数为4. 那么数________所表示的点是![]() 的优点;(直接填在横线上)
的优点;(直接填在横线上)
(2)如图3,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为40. 现有一只电子蚂蚁
所表示的数为40. 现有一只电子蚂蚁![]() 从点
从点![]() 出发,以4个单位每秒的速度向左运动,到达点
出发,以4个单位每秒的速度向左运动,到达点![]() 停止. 当
停止. 当![]() 为何值时,
为何值时,![]() 、
、![]() 和
和![]() 中恰有一个点为其余两点的优点?
中恰有一个点为其余两点的优点?
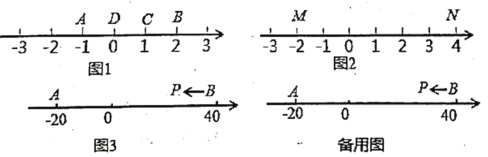
【答案】(1) 2或10;(2) 当t为5秒、10秒或7.5秒时,P、A和B中恰有一个点为其余两点的优点.
【解析】
(1)设所求数为x,根据优点的定义分优点在M、N之间和优点在点N右边,列出方程解方程即可;
(2)根据优点的定义可知分两种情况:①P为(A,B)的优点;②P为(B,A)的优点;③B为(A,P)的优点.设点P表示的数为![]() ,根据优点的定义列出方程,进而得出t的值.
,根据优点的定义列出方程,进而得出t的值.
(1)设所求数为x,
当优点在M、N之间时,由题意得:![]() ,
,
解得![]() ;
;
当优点在点N右边时,由题意得:![]() ,
,
解得:![]() ;
;
故答案为:2或10;
(2)设点P表示的数为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
分三种情况:
①P为![]() 的优点,
的优点,
由题意,得![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴![]() (秒);
(秒);
②P为![]() 的优点,
的优点,
由题意,得![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴![]() (秒);
(秒);
③B为![]() 的优点,
的优点,
由题意,得![]() ,即
,即![]() ,
,
解得:![]() ,
,
此时,点P为AB的中点,即A也为![]() 的优点,
的优点,
∴![]() (秒);
(秒);
综上可知,当t为5秒、10秒或7.5秒时,P、A和B中恰有一个点为其余两点的优点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
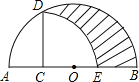
【题目】如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗洪抢险救灾中,某地粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到没有受洪水威胁的A,B两仓库,已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为60吨,B库的容量为120吨,从甲、乙两库到A、B两库的路程和运费如表(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
若从甲库运往A库粮食x吨,
(Ⅰ)填空(用含x的代数式表示):
①从甲库运往B库粮食 吨;
②从乙库运往A库粮食 吨;
③从乙库运往B库粮食 吨;
(Ⅱ)写出将甲、乙两库粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式,并求出当从甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M,N分别是AC,BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任一点,满足AC+CB=a cm,其他条件不变,你能猜想MN的长度吗?(用含a的代数式表示)并说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店经销进价分别为![]() 元/千克、
元/千克、![]() 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
时间 | 甲水果销量 | 乙水果销量 | 销售收入 |
周五 |
|
|
|
周六 |
|
|
|
(1)求甲、乙两种水果的销售单价;
(2)若水果店准备用不多于![]() 元的资金再购进两种水果共
元的资金再购进两种水果共![]() 千克,求最多能够进甲水果多少千克?
千克,求最多能够进甲水果多少千克?
(3)在(2)的条件下,水果店销售完这![]() 千克水果能否实现利润为
千克水果能否实现利润为![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
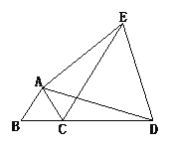
【题目】已知:如图,△ABC为正三角形,D是BC延长线上一点,连结AD,以AD为边作等边三角形ADE,连结CE,用你学过的知识探索AC、CD、CE三条线段的长度有何关系?试写出探求过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com