
分析 (1)根据平行线的判定和性质证明即可;
(2)根据左边角的和等于右边角的和解答即可;
(3)根据平移性质和三角形面积公式进行解答.
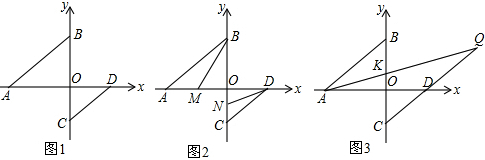
解答 证明:(1)过点O作OE∥AB,
∵AB∥CD,
∴OE∥CD(平行公理的推论),
∴∠ABO=∠BOE,∠CDO=∠DOE,
∴∠ABO+∠CDO=∠BOE+∠DOE=∠BOD=90°;
(2)“猪蹄模型”中左边角的和等于右边角的和,即∠ABM+∠ODN=∠CDN+∠OBM,
设∠ABM=∠OBM=x,∠ODN=∠CDN=y,
∴x+y=$\frac{1}{2}$(∠ABO+∠CDO)=45°,
∴∠BMO+∠OND=x+y+90°=135°,
(3)线段CQ可看作是由线段AB平移得到,
∵A(-4,0)→C(0,a),
∴B(0,3)→D(4,3+a),
设K点的坐标为(0,y),
S△AOQ=$\frac{1}{2}$×4×(3+a)=2(3+a),S△AOK=2y,S△QOK=2y,
由S△AOQ=S△AOK+S△QOK,
∴2y+2y=2(3+a),解得y=$\frac{3+a}{2}$,
∴BK=3-$\frac{3+a}{2}$=$\frac{3-a}{2}$,OK=$\frac{3+a}{2}$,OC=-a,
∴$\frac{BK-OK}{OC}$=1.
点评 此题考查三角形的内角和定理,关键是根据三角形的内角和定理和平行线的判定以及性质进行解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
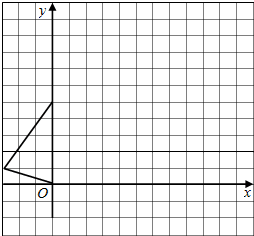 如图,已知△OAB的三个顶点的坐标分别为O(0,0)、A(-3,1)、B(0,5),三角形内有任意一点P坐标为(a,b)
如图,已知△OAB的三个顶点的坐标分别为O(0,0)、A(-3,1)、B(0,5),三角形内有任意一点P坐标为(a,b)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
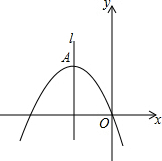 如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.
如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com