
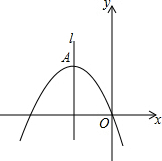
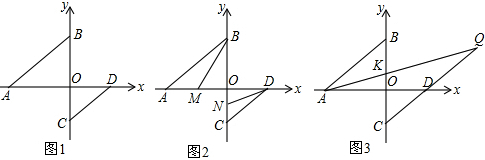
 如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.
如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.分析 (1)根据二次函数图象的顶点设出二次函数的关系式,再很据二次函数图象经过原点,求出a的值,即可得出二次函数的关系式;
(2)设直线OP的解析式为y=kx,将A点代入,求出直线OP的解析式,再把x=-4代入y=-$\frac{1}{2}$x,求出M的坐标,根据点M、N关于点P对称,求出N的坐标,从而得出MN的长,再根据三角形的面积公式即可得出答案.
(3)①设对称轴l交x轴于点B,作PC⊥l于点C,由P在二次函数图象上,设P$(t,-\frac{1}{4}{t^2}-2t)$,再由O的坐标,表示出直线OP的解析式,进而表示出M,N及H的坐标,设对称轴l交x轴于点B,作PC⊥l于点C,构建相似三角形:△NCP∽△NBO.由相似三角形的对应角相等证得结论;
②△OPN能为直角三角形,理由为:分三种情况考虑:若∠ONP为直角,由①得到∠PNM=∠ONM=45°,可得出三角形ACN为等腰直角三角形,得到PC=CN,将表示出的PC及CN代入,得到关于m的方程,求出方程的解得到m的值为0或4±$\sqrt{2}$,进而得到此时A与P重合,不合题意,故∠ONP不能为直角;若∠PON为直角,利用勾股定理得到OP2+ON2=PN2,由P的坐标,利用勾股定理表示出OP2,由OB及BN,利用勾股定理表示出ON2,由PC及CN,利用勾股定理表示出PN2,代入OP2+ON2=PN2,得到关于m的方程,求出方程的解得到m的值为4±4$\sqrt{2}$或0,然后判断∠PON是否为直角;若∠NPO为直角,则有△PMN∽△BMO∽△BON,由相似得比例,将各自的值代入得到关于m的方程,求出方程的解得到m的值为4,此时A与P重合,故∠NPO不能为直角,综上,点P在对称轴l左侧的二次函数图象上运动时,△OPN不能为直角三角形.
解答 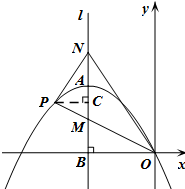
 (1)解:设二次函数的表达式为y=a(x+4)2+4,
(1)解:设二次函数的表达式为y=a(x+4)2+4,
把点(0,0)代入表达式,解得$a=-\frac{1}{4}$.
∴二次函数的表达式为$y=-\frac{1}{4}{(x+4)^2}+4$,
即$y=-\frac{1}{4}{x^2}-2x$;
(2)解:设直线OP为y=kx(k≠0),
将P(-6,3)代入y=kx,解得$k=-\frac{1}{2}$,
∴$y=-\frac{1}{2}x$.
当x=-4时,y=2.
∴M(-4,2).
∵点M、N关于点A对称,
∴N(-4,6).
∴MN=4.
∴S△PON=S△OMN+S△PMN=12;
(3)①证明:设点P的坐标为$(t,-\frac{1}{4}{t^2}-2t)$,
其中t<-4,
设直线OP为y=k′x(k′≠0),
将P$(t,-\frac{1}{4}{t^2}-2t)$代入y=k′x,解得$k'=-\frac{t+8}{4}$.
∴$y=-\frac{t+8}{4}x$.
当x=-4时,y=t+8.
∴M(-4,t+8).
∴AN=AM=4-(t+8)=-t-4.
设对称轴l交x轴于点B,作PC⊥l于点C,
则B(-4,0),C$(-4,-\frac{1}{4}{t^2}-2t)$.
∴OB=4,NB=4+(-t-4)=-t,PC=-4-t,
NC=$-t-(-\frac{1}{4}{t^2}-2t)$=$\frac{1}{4}{t^2}+t$.
则$\frac{NC}{PC}=\frac{{\frac{1}{4}{t^2}+t}}{-4-t}=-\frac{t}{4}$,$\frac{NB}{OB}=\frac{-t}{4}=-\frac{t}{4}$.
∴$\frac{NC}{PC}=\frac{NB}{OB}$.
又∵∠NCP=∠NBO=90°,
∴△NCP∽△NBO.
∴∠PNM=∠ONM.
②△OPN能为直角三角形,理由如下:
解:分三种情况考虑:
(i)若∠ONP为直角,由①得:∠PNM=∠ONM=45°,
∴△PCN为等腰直角三角形,
∴CP=NC,即m-4=$\frac{1}{4}$m2-m,
整理得:m2-8m+16=0,即(m-4)2=0,
解得:m=4,
此时点A与点P重合,故不存在P点使△OPN为直角三角形;
(ii)若∠PON为直角,根据勾股定理得:OP2+ON2=PN2,
∵OP2=m2+(-$\frac{1}{4}$m2-2m)2,ON2=42+m2,AN2=(m-4)2+(-$\frac{1}{4}$m2-2m+m)2,
∴m2+(-$\frac{1}{4}$m2-2m)2+42+m2=(m-4)2+(-$\frac{1}{4}$m2-2m+m)2,
整理得:m(m2-8m-16)=0,
解得:m=0或m=-4-4$\sqrt{2}$或-4+4$\sqrt{2}$(舍去),
当m=0时,P点与原点重合,故∠PON不能为直角,
当m=-4-4$\sqrt{2}$,即P(-4-4$\sqrt{2}$,4)时,N为第四象限点,成立,故∠PON能为直角;
(iii)若∠NPO为直角,可得∠NPM=∠OBM=90°,且∠PMN=∠BMO,
∴△PMN∽△BMO,
又∵∠MPN=∠OBN=90°,且∠PNM=∠OND,
∴△PMN∽△BON,
∴△PMN∽△BMO∽△BON,
∴$\frac{MB}{OB}$=$\frac{OB}{NB}$,即$\frac{8-m}{4}$=$\frac{4}{m}$,
整理得:(m-4)2=0,
解得:m=4,
此时A与P重合,故∠NPO不能为直角,
综上,点P在对称轴l左侧的二次函数图象上运动时,△OPN能为直角三角形,当m=4+4$\sqrt{2}$,即P($-4-4\sqrt{2},-4$)时,N为第四象限的点成立.
点评 此题考查了利用待定系数法求二次函数解析式,两点坐标确定一次函数解析式,相似三角形的判定与性质,等腰直角三角形的判定与性质,勾股定理,以及相似三角形的判定与性质,本题(3)中的第②小问利用的是反证法,先假设结论成立,利用逻辑推理的方法得出与已知条件,定理,公理矛盾,可得出假设错误,原结论不成立.


科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:单选题
画△ABC中AC边上的高,下列四个画法中正确的是( )
A.  B.
B. 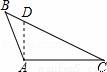
C. 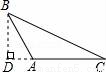 D.
D. 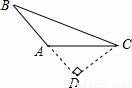
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
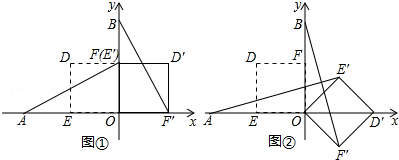
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
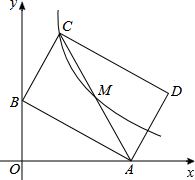 如图,已知:直线y=-$\frac{1}{3}$x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=$\frac{k}{x}$(x>0)正好经过C,M两点,则k=4.
如图,已知:直线y=-$\frac{1}{3}$x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=$\frac{k}{x}$(x>0)正好经过C,M两点,则k=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
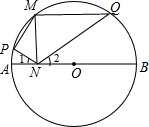 如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P,Q分别为弧AM,弧BM上一点(不与端点重合),如果∠MNP=∠MNQ.有以下结论:①∠1=∠2,②∠MPN+∠MQN=180°,③∠MQN=∠PMN,④PM=QM,⑤MN2=PN•QN.其中正确的是①③⑤.
如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P,Q分别为弧AM,弧BM上一点(不与端点重合),如果∠MNP=∠MNQ.有以下结论:①∠1=∠2,②∠MPN+∠MQN=180°,③∠MQN=∠PMN,④PM=QM,⑤MN2=PN•QN.其中正确的是①③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
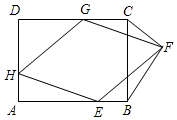 已知,如图,矩形ABCD中,AD=6,DC=10,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF、BF.
已知,如图,矩形ABCD中,AD=6,DC=10,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF、BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com